PROBLEMA DEL aceite y el vinagre

Un astuto especulador se inicia en los negocios con un lote de barriles de aceite y vinagre. No sabemos cuantos barriles hay de cada uno pero sabemos que su primer cliente pagó $14 por cierta cantidad de galones de aceite y $14 por cierta cantidad de galones de vinagre y que pagó el doble por el galón de aceite que por el de vinagre, finalmente le dejó un solo barril.

¿qué barril deja?

Solución

El cliente compró los barriles de aceite de 13 y 15 galones a 50 centavos por galón, y los barriles de vinagre de 31, 17 y 8 galones a veinticinco centavos por galón. Esto deja al barril de 19 galones, que puede contener tanto aceite como vinagre. 


See more at: http://www.puzzleclopedia.com/el-aceite-y-el-vinagre/#sthash.aYZMjwen.dpuf

PROBLEMA INTERESANTE

¿Qué pasaría si...

... cortáramos un cubo con un plano? ¿Podríamos obtener un triángulo semejante a cualquier triángulo dado?

SOLUCIÒN

Recordemos en primer lugar que dos triángulos son semejantes si los cocientes de los lados correspondientes son todos iguales a un número fijo. Por ejemplo, la Figura 1 muestra dos triángulos semejantes:

Figura 1.

Estos dos triángulos satisfacen las relaciones

Una vez hecha esta aclaración, la respuesta a la pregunta es que no es posible obtener un triángulo semejante a cualquier triángulo dado. Por ejemplo, veamos que este proceso de cortar el cubo con un plano no nos puede dar un triángulo recto. En la Figura 2 se ve un posible corte.

Figura 2.

Los tres triángulos que aparecen en otras tantas caras del cubo son rectos, por lo cual sabemos que se cumplen las siguientes relaciones:

Si además queremos que se cumpla, digamos, la relación , usando las tres relaciones anteriores podemos escribir:

de donde resulta , lo cual está claro que no puede ser. Desde luego, llegaríamos a una contradicción semejante si supusiéramos que el lado    ó el   es la hipotenusa del triángulo.

En este tema de cortar un cubo con un plano se pueden hacer muchas otras preguntas. Por ejemplo, ¿es posible obtener triángulos isósceles o equiláteros?, ¿es posible obtener un cuadrado o un rectángulo?, ¿se puede tener una sección pentagonal o hexagonal?, ¿qué polígonos regulares se pueden obtener?

Una manera divertida de experimentar es cortando patatas en forma de cubos y luego cortando los cubos de diferentes maneras. Los cortes, sumergidos en pintura, se convierten en sellos que pueden forman efectos interesantes sobre una hoja de papel.

	Sobre la autora
	Josefina (Lolina) Álvarez es Professor of Mathematics en New Mexico State University (USA). Especialista en análisis armónico y funcional, se doctoró en Matemáticas por la Universidad de Buenos Aires (Argentina), bajo la dirección de A.P. Calderón TOMADO DE: http://www.matematicalia.net/index.php?option=com_content&task=view&id=452&Itemid=275

MÈTODO DEL CANGREJO

Metodo cangrejo from Reynaldo Humberto Vera Yampi

CUATRO PREGUNTAS DE MATEMÁTICAS

1. ¿Cómo cortar el queso?   Los aficionados al queso de Camembert saben que este suele presentarse en piezas discoidales. Saben también que suele cortarse en sectores para su consumo, y que al dejar parte del queso cortado y sin consumir,la zona del del corte se seca y pierde su delicioso sabor. Procede pues, si no vamos a terminar en un día todo el disco de queso, cortarlo de la forma más eficaz posible para evitar pérdidas. Centraremos nuestra atención en el caso de que deseemos hace porciones del mismo tamaño. El problema, matemáticamente, se planteará así: Dado un círculo de radio unidad, ¿cómo dividirlo en n partes de la misma área de forma que el perímetro fronterizo sea de la menor longitud posible?
2. ¿Discriminación?Una empresa es acusada por un sindicato de discriminación sexual por contratar mayor proporción de hombres que de mujeres. La empresa alega que el promedio de contratación de mujeres en cada departamento es siempre mayor que el de hombres. Las afirmaciones de la empresa y del sindicato parecen contradictorias, pero, ¿podría suceder que ninguno mintiera?
3. Otra de naipes.Tomamos una baraja, volvemos la primera carta, la siguiente la colocamos debajo del mazo, volvemos la siguiente carta, la siguiente la volvemos a poner debajo y seguimos así hasta que estén todas vueltas. Resulta que las cartas han salido en orden creciente, primero oros, luego copas, luego espadas y finalmente bastos. ¿Cómo estaban colocadas en un principio?
4. Uno de cinemática.Dados dos puntos A y B situados en un plano vertical, encontrar otro punto C del mismo plano tal que dos móviles que parten de A y B simultáneamente cayendo por planos inclinados AC y BC se encuentren en C en un tiempo mínimo

SOLUCIONES:

1. Para n=2 ó n=3 las soluciones con triviales: el corte se hará según un diámetro en el primer caso, y según tres sectores de 120 grados en el segundo. 

Pero para n=4 la cosa comienza ya a complicarse. Pues un corte según cuatro sectores de noventa grados arrojaría una longitud de corte L=4, mientras que en el sistema indicado en la figura de la izquierda basta con L=3,9624. 

Esta división se ha obtenido recordando la conocida propiedad de que el punto situado en el interior de un triángulo cuya suma de distancias a los tres vértices es mínima es el que ve estos bajo ángulos de 120 grados. Sin embargo, todavía puede mejorarse: intuitivamente se comprende que, al no ser los segmentos rectos incidentes sobre la circunferencia perpendiculares a ésta podrían ser sustituídos por arcos de circunferencia que cumplieran con esta condición. Se mejora todavía algo, llegando a la figura de la derecha donde L=3,9412.

2.  Ambas entidades pueden tener razón porque más importantes que los promedios en sí mismos son las cantidades que dieron origen a esos promedios. Para ilustrarlo, lo mejor un ejemplo. En el departamento A se contrataron 4 de las 8 mujeres presentadas y 32 de los 80 hombres presentados. En el departamento B se contrataron 10 de las 40 mujeres presentadas y 4 de los 20 hombres. 

Estos datos conducen a un 50% y un 40% de contratación para mujeres y hombres en el departamento A, y un 25% y un 20% respectivamente, para el departamento B. En conjunto, la empresa ha contratado a 14 de las 48 mujeres (29,1%) y a 36 de los 100 hombres con lo que vemos que ambas afirmaciones eran ciertas.

3. Para explicarlo voy a suponer que sólo tengo las 10 cartas de un palo. La solución es fácilmente generalizable a cualquier número de cartas. 

Pensemos en que tenemos diez lugares en los que debemos ir colocando la carta adecuada. Es evidente que que los lugares primero, tercero, quinto, séptimo y noveno deberán estar ocupados por el As, 2, 3, 4 y 5. Una vez colocada la primera carta, el proceso que se ha seguido consiste en dejar un hueco y colocar la siguiente carta. Este es el proceso que deberemos aplicar hasta el final, pasar por alto un hueco y colocar la carta en el hueco siguiente. Por hueco entiendo cada uno de los lugares iniciales que aún están libres. 

Una vez colocado el 5 en el noveno lugar dejamos pasar el hueco décimo y ponemos el 6 en el siguiente hueco que es el segundo. Dejamos pasar el cuarto y colocamos el 7 en el sexto. Saltamos el octavo y ponemos la sota en el décimo y finalmente ponemos en rey en el cuarto. 

Las cartas de arriba a abajo, quedarían colocadas del siguiente modo: As, 6, 2, Rey, 3, 7, 4, Caballo, 5, Sota. 
Este procedimiento es extrapolable a cualquier número de cartas y generalizable para cualquier relación cartas vueltas/ cartas puestas.

4.  Para este problema se han recibido soluciones basadas en álgebra, pero resultan algo largas. Puede ser una buena ocasión para recordar el teorema de las esferas isocronas, tan útil en casos como éste, y que parece algo olvidado. Como es fácil comprobar, un móvil partiendo mediante un plano inclinado del polo N de una esfera alcanza cualquier punto de ésta en el mismo tiempo t = 2(R/g)½. 

En el caso precedente, las dos esferas centradas en Oa y Ob deberán tener el mismo radio. La condición de tiempo mínimo exige que sean tangentes, así que dicho radio será la mitad de la distancia AB, igual, por paralelismo, a la OaOb. 

 

TOMADO DE: 

http://www.mensa.es/juegosmensa/e031035.html

http://www.mensa.es/juegosmensa/s031035.html#SOLU031

GEOMETRÍA RECREATIVA

Dos métodos más 
Sepueden medir las alturas sin ayuda de las sombras. Existen diversas formas;empezaremos examinando dos de ellas, bastante simples.
Parainiciar podemos emplear las propiedades del triángulo rectángulo isósceles,utilizando un sencillo instrumento, el cual se construye con suma facilidad,con una tablilla y tres alfileres. Sobre una tablilla lisa marcamos trespuntos, los vértices del triángulo rectángulo isósceles, en estos puntosclavamos los alfileres (Figura 4).

Figura 4. El instrumento hecho con alfileres para medir alturas

Si nodispone de escuadra y compás para dibujar el triángulo, puede coger un papel,lo dobla una vez, lo dobla luego en sentido transversal respecto al primerdoblez, de modo que se unan los extremos del mismo, de este modo se obtiene elángulo recto. Se puede emplear el mismo papel para medir los trazos ab y bc, demodo que tengan igual longitud.
Comovemos, podemos construir el instrumento de diversas formas.
Esteinstrumento es tan fácil de usar como de construir. Alejándose del árbol,coloque el instrumento de modo que uno de los catetos del triángulo se orienteverticalmente. Para facilitar la medición, puede utilizar una plomada (un hilocon un objeto pesado atado a un extremo) atada al alfiler superior de estecateto.

Figura 5. Esquema del uso de la tablilla con alfileres.

Acercándoseal árbol o alejándose de él, encontrará un sitio A (Figura 5), desde el cual,verá que los alfileres a y c, tapan la copa C del árbol: eso significa que laprolongación de la hipotenusa ac pasa por el punto C. Como ya lo hemos visto enel ejemplo anterior, la separación entre ab es igual a CB, ya que el ángulo α= 45°.
Finalmente,después de medir el trazo aB y agregarle la longitud de BD, equivalente a laaltura aA de los ojos al piso, se obtiene la altura del árbol.
Existeotro método, que no usa la tablilla con los alfileres. Usted necesita un jalón;se clava verticalmente éste en la tierra de modo que la parte que sobresalgadel piso sea igual a su estatura. Debe elegir el sitio para el jalón de modoque le permita, al tumbarse como se muestra en la Figura 6, ver la copa delárbol y el punto superior del jalón en línea recta.

Figura 6. Otro método más para medir la altura.

Comoel triángulo Aba, es isósceles y rectangular, entonces el ángulo A = 45°, y porlo tanto AB = BC, es la altura buscada del árbol.

3. El método de Julio Verne 
El siguientemétodo también es sencillo. Julio Verne describió en su novela “La islamisteriosa” la forma de medir los objetos de gran altura:
– Hoyvamos a medir la altura del acantilado de Vista Lejana, –dijo el ingeniero.
–¿Necesitamos algunos instrumentos? –preguntó Gebert.
– Nohace falta. Lo haremos de otra manera, más fácil y más segura.
Eljoven, caminó desde el acantilado hasta la orilla. Cogió un jalón de 12 pies delongitud, el ingeniero comprobó la medida con su estatura, la cual conocíabien. Gebert entregó una plomada al ingeniero; ésta no era más que una piedraatada al extremo de una cuerda. Situándose a 500 pies del acantilado vertical,el ingeniero clavó el jalón verticalmente en la arena, con la ayuda de laplomada, enterrándola a dos pies de profundidad. Luego se alejó del jalón,hasta que tumbándose en el suelo pudo ver el extremo saliente del jalón y lacresta del acantilado en línea recta (Figura 7). Marcó este punto con unaestaca.
–¿Tienes algunas nociones de geometría?– preguntó a Gebert.
– Sí.
–¿Recuerdas las propiedades de los triángulos semejantes?
– Suslados correspondientes son proporcionales.
–Exacto. Ahora voy a construir dos triángulos rectángulos semejantes. Un catetodel triángulo pequeño será el jalón, el otro cateto, será la distancia desde laestaca hasta el pie del jalón; la hipotenusa, es mi línea de vista. En eltriángulo mayor los catetos son el acantilado, cuya altura queremos medir, y ladistancia desde la estaca hasta el pie del acantilado; la hipotenusa es milínea de vista, que se une con la hipotenusa del triángulo menor.

Figura 7. Como encontraron la altura de un acantilado los personajes de Julio Verne

– ¡He entendido! – exclamó el joven. La distancia de la estaca hasta el jalón es a la distancia desde la estaca hasta el pie del acantilado, como la altura del jalónes a la altura del acantilado.
–Exactamente. Sigamos, si medimos las dos primeras distancias, y sabemos la altura del jalón, podemos calcular el cuarto miembro de la proporción que es la altura del acantilado.
Se midieron ambas distancias horizontales: la pequeña midió 15 pies, la grande                                                                                      midió 500 pies.
Finalmenteel ingeniero anotó:

15 : 500 = 10 : x

15 x = 500 x 10

x=333,3 pies

Entonces,la altura del acantilado es de 333 pies.

TOMADO DE: http://www.librosmaravillosos.com/geometriarecreativa/capitulo01.html

PREGUNTAS DE RAZONAMIENTO MATEMÁTICO

                                              EL PROBLEMA DEL ANDARÍN

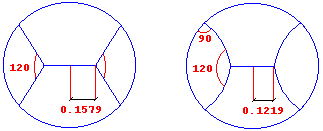
Se trata de un hombre de 1,80 m . de estatura que camina sobre el Ecuador y da así toda la vuelta a la Tierra , ¿qué longitud habrá recorrido más su cabeza que sus pies?. ¿Y si lo hace sobre el ecuador de la Luna ?.

Solución:

L. cabeza = 

L. pies = 

Diferencia de longitudes = 

11,31 metros

Dando la vuelta a cualquier esfera, la respuesta es la misma.

TRES AMIGOS EN EL BAR

Os voy a contar una vieja historia que muy bien pudiera ser real:
Van tres amigos a tomarse un refresco. Después de tomarlo, al pedir la cuenta, es donde viene el lío:
- Amigos : Camarero, nos trae la cuenta, por favor.- Camarero: Son 300 pesetas, caballeros.
Y cada uno de ellos pone 100 pesetas.
Cuando el camarero va a poner el dinero en caja, lo ve el jefe y le dice:
- Jefe : No, esos son amigos míos. Cóbrales solo 250 ptas.
 
El camarero se da cuenta que si devuelve las 50 ptas. puede haber problema para repartirlas y decide lo siguiente:
- Camarero: Ya está. Me quedaré 20 ptas. y les devuelvo 30, diez para cada uno.
Les devuelve a cada uno 10 ptas.
Ahora es cuando viene el follón. Si cada uno puso 100 ptas. y le devuelven 10 ptas, realmente puso cada uno de ellos 90 ptas.
90 x 3 = 270 ptas. Si añadimos las 20 que se queda el camarero, 290 ptas.......
¿ DÓNDE ESTÁN LAS OTRAS 10 PESETAS ?

Solución:

Este es un caso típico de cómo se pueden enredar las cosas.

Lo correcto es decir que 250 ptas. fueron a caja y 20 ptas. es la propina del camarero.

ENGAÑOSO PROMEDIO: LOS AUTOMOVILISTAS

Pedro y Pablo son dos automovilistas que hacían habitualmente el mismo viaje de ida y vuelta entre dos ciudades, cada uno en su coche.
En cierta ocasión hablaron del asunto y Pedro dijo a Pablo:
- El viaje de ida lo hago a 80 km/h y la vuelta a 60 km/h .
Pablo contestó a Pedro: - Por las características de mi coche y de la carretera, hago el viaje de ida y vuelta a la velocidad constante de 70 km/h , que es el promedio de las velocidades que Vd. me ha dicho, de modo que empleamos el mismo tiempo en el viaje.
¿El razonamiento de Pablo es correcto?. ¿Emplean el mismo tiempo en el viaje?

Solución:

Pablo emplea menos tiempo en hacer el viaje.

Supongamos que la distancia entre las ciudades es 100 km:

Pedro :

•  En la ida: t = e/v ; t = 100 km / 80 km/h = 5/4 horas

• En la vuelta: t = 100 km / 60 km/h = 5/3 horas

Tiempo total: 2 horas y 55 minutos

Pablo:

•  t = e/v ; t = 200 km / 70 km/h = 2 horas y 51 minutos.

                                    DOS CICLISTAS Y UNA MOSCA

Dos ciclistas parten de dos ciudades distantes entre sí 50 km . al encuentro el uno del otro a la velocidad de 25 km/h . Una mosca sale desde una de las bicicletas hacia la otra, volando a 42 km/h .

Cuando encuentra a la otra, regresa hacia la primera, siempre a la misma velocidad; así hasta que los dos ciclistas se encuentran. ¿Cuántos kilómetros ha recorrido la mosca en este vaivén?

Solución

 Está claro que los ciclistas que están a 50 km . el uno del otro, y que circulan a 25 km/h , se encuentran en UNA hora, es el mismo tiempo que está la mosca volando de una bicicleta a otra a la velocidad de 42 km/h , por tanto recorrerá 42 kilómetros .

LA MADRE DE TODAS LAS BATALLAS

Lewis Carroll, matemático y escritor británico cuyo verdadero nombre es Charles Lutmidge Dogson lo conocemos principalmente por su obra "Alicia en el país de las maravillas", y siempre ha manifestado su interés por lo absurdo, los acertijos y la confusión.

Un problema que se atribuye a él es el siguiente:

 En una extraordinaria batalla, por lo menos el 70% de los combatientes perdió un ojo; el 75% una oreja, por lo menos el 80% perdió una mano y el 85% una pierna. ¿Cuántos, por lo menos perdieron los cuatro órganos?

Solución:

 Por lo menos el 45% perdió el ojo y la oreja:

 Por lo menos el 65% perdió la mano y la pierna:

 Por lo menos el 10% perdió los cuatro órganos:

tomado de: http://joseealvarezn.galeon.com/curiosidad.htm

Curiosidades con cuadrados

Los cuadrados

Una particularidad de los cuadrados es que el cuadrado de un número n es igual a la suma de los números impares de 1 a sn-1

1² = 1
2² = 1 + 3 
3² = 1 + 3 + 5
4² = 1 + 3 + 5 + 7
5² = 1 + 3 + 5 + 7 + 9
6² = 1 + 3 + 5 + 7 + 9 + 11
7² = 1 + 3 + 5 + 7 + 9 + 11 + 13
8² = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15
9² = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17
10² = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19

Esto también puede traducirse en el siguiente dibujo:

Otra sucesión piramidal sería la de los números naturales elevados al cubo:

1³ = 1
2³ = 3 + 5 
3³ = 7 + 9 + 11
4³ = 13 + 15 + 17 + 19
5³ = 21 + 23 + 25 + 27 + 29
...

---

Más curiosidades:

• La diferencia entre los cuadrados de dos números consecutivos es igual al doble del número más pequeño más uno:
  71² - 70² = (70 x 2) + 1
• El cuadrado más pequeño posible formado con las 9 primeras cifras es 139.854.276 = 11.826² y el cuadrado más grande posible es 923.187.456 = 30.384²



• El cuadrado más pequeño posible formado con las diez primeras cifras es: 1.026.753.849 = 32.043² y el cuadrado más grande posible es: 9.814.072.356 = 99.066²
  
• La suma de 3 potencias de de 2 consecutivas, es igual al valor de la primera potencia por 7: 2² + 2³ + 2⁴ = 4 * 7 = 28
  2⁵ + 2⁶ + 2⁷ = 32 * 7 = 28
  
• El número 365 es un número curioso ya que es el único que cumple con la propiedad:
  
  10² + 11² + 12² = 13² + 14² = 365

---

Multigrado curioso:

tomado de:http://www.acertijos.net/curiosidades-matematicas-2.html