TOMADO DE: http://ecuacionesonline.blogspot.com/2010/10/humor-matematico-grafico.html
MATEMÁTICA PARA TODOS
jueves, 7 de agosto de 2014
ILUSIÓN ÓPTICA N° 3
TOMADO DE:http://vasitorojo.blogspot.com/2013/10/ilusiones-opticas-que-no-te-vas-creer.html
Sobre el patrón de los números primos
Determinación geométrica de los números primos y perfectos.
Omar E. Pol
Introducción
Desde hace 2500 años los números primos atraen la atención de matemáticos y aficionados de todo el mundo, por varias razones. Una de ellas es la fascinación que produce su irregular distribución a lo largo de la recta numérica. Los números primos aparecen esparcidos aquí y allá, encontrándose sectores en donde abundan y otros en donde escasean. Se los califica de misteriosos e indomables pues no parece existir ninguna regla que determine su ubicación entre los demás números naturales. Si bien no hay una fórmula que prediga la distancia entre un primo y otro, cabe preguntarse lo siguiente: ¿Acaso no es la superposición de distintos patrones regulares lo que produce esa irregularidad? Por otro lado, sabemos que entre los primeros 30 millones de números naturales sólo se encuentran 4 números perfectos: 6, 28, 496 y 8128. El quinto lugar lo ocupa un número de 8 dígitos: 33550336. Nos preguntamos ¿Cuál es el patrón geométrico subyacente que origina esta extraña serie? ¿Acaso hay que relacionar varios patrones distintos para resolver este problema?
En este breve ensayo se describe la geometría que determina la distribución exacta de los números primos y también de los números perfectos. Se ilustra el texto con 16 diagramas originales dibujados (o borroneados) por el autor. A continuación se repasan algunos conceptos básicos sobre números naturales, luego se muestra el modelo principal y algunos de sus derivados con formas recreativas, posteriormente se construye una función sencilla que genera la serie de números primos y por último se describe el patrón geométrico de los números perfectos.
Conceptos básicos
Los números naturales son los números que utilizamos a diario para contar: 1, 2, 3, 4, 5, 6, etc. Están formados por el número 1, los números primos y los números compuestos. Los números primos son los números que tienen 2 divisores: Sólo pueden dividirse en forma exacta por la unidad y por sí mismos. Entre los primeros 10 números naturales encontramos 4 primos: 2, 3, 5 y 7. Del 1 al 100 hay 25 primos. Del 1 al 1000 hay 168 y a medida que avanzamos por la recta se hacen cada vez más escasos, siendo su distribución muy irregular. Los números primos son importantes porque son los átomos de la Matemática. Todos los demás números se construyen a partir de ellos. Los números primos (prime numbers, en inglés) son infinitos como lo demostró Euclides alrededor del año 300 A.C. Los primos menores que 10 son extraordinarios: El 2 es el único primo par. El 2 y el 3 son los únicos primos contiguos. El 5 es el único primo terminado en 5. Por último: 3, 5 y 7 forman la única tríada de primos gemelos en toda la recta numérica. Las lagunas, desiertos o boquetes son los sectores de la recta numérica en donde no aparece ningún primo. Por ejemplo; una pequeña laguna está localizada en el intervalo que contiene a los números 8, 9 y 10. Se sabe que éstas regiones formadas por números compuestos pueden llegar a tener cualquier longitud que se desee. Los números compuestos son los que tienen más de 2 divisores. Los divisores de un número son los números que pueden dividirlo en forma exacta (Sin generar resto). Por ejemplo: Los divisores del 4 son: 1, 2 y 4. Los divisores del 6 son: 1, 2, 3 y 6. Entre los primeros 10 números naturales se encuentran los siguientes compuestos: 4, 6, 8, 9 y 10.
La criba de Eratóstenes es un antiguo y efectivo método para hallar números primos. Consiste en una tabla de números naturales dispuestos en columnas. Primero se tachan todos los múltiplos de 2. Luego se tachan todos los múltiplos del siguiente número no tachado anteriormente y así sucesivamente. Los números que quedan sin tachar son los números primos. Para determinar si un número es primo se sabe que no hace falta dividirlo por todos los números menores a él. Basta con dividirlo por los números impares mayores que 1 y menores o iguales a la raíz cuadrada del número. Si no se encuentra ningún divisor entonces el número es primo. Si se encuentra un divisor, o si el número es par y mayor que 2, entonces el número es compuesto.
La criba de 30 columnas
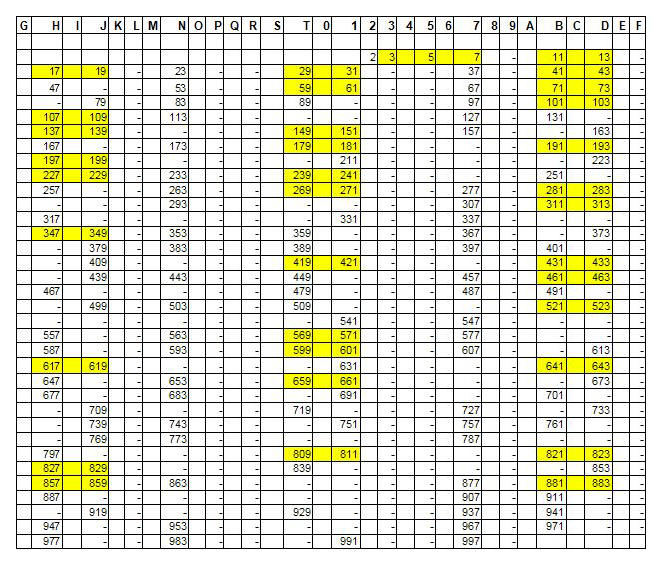Fig. 1. En la tabla aparecen ordenados los 3 tipos de parejas de primos gemelos.
Un intento de percibir algún patrón subyacente en la distribución de los números primos es la construcción de una criba formada por 30 columnas. La tabla muestra en forma ordenada los 3 tipos de parejas de primos gemelos. Estos son los primos que están separados por un número. Por ejemplo: (11 y 13), (17 y 19), (29 y 31), etc. En la tabla, no figuran los números pares mayores que 2 y las posiciones de los números compuestos impares están identificadas con un guión. Nótese que la serie de números primos comienza recién en la mitad de la primera fila de la tabla. Con ello se logra un ordenamiento mucho mayor que con otros tipos de tablas. Las tablas con menor cantidad de columnas no pueden mostrar separadas y ordenadas las 3 clases de primos gemelos y en las tablas con mayor cantidad de columnas las parejas de primos gemelos aparecen desordenadas o en columnas duplicadas.
Nótese que los números primos mayores que 10 sólo pueden aparecer en las columnas 1, 7, B, D, H, J, N y T. Estos caracteres alfanuméricos corresponden a las terminaciones de los números primos si, en lugar de expresarlos con un sistema decimal, se los expresa con un sistema de 30 caracteres o trígesimal.
Clasificación de números primos
En la tabla anterior se distinguen, en general, 3 clases de primos. Por lo tanto se puede intentar una clasificación al dividirlos en primos gemelos, primos casi-gemelos y primos solitarios.
Los primos gemelos pueden formar 3 tipos de parejas cuyas terminaciones son: (7,9); (9,1) y (1,3).:
Los primos casi-gemelos son los primos que están en las columnas de primos gemelos pero les falta el compañero. La serie de primos casi-gemelos comienza con: 47, 79, 89, 131, 163, 167...
Los primos solitarios se hallan en las columnas 7 y N de la tabla y se clasifican en 2 tipos cuyas terminaciones son 3 y 7. Los primos solitarios no pueden ser gemelos porque su compañero es divisible por 5. La serie de primos solitarios comienza con: 23, 37, 53, 67, 83, 97,113, 127, 157...
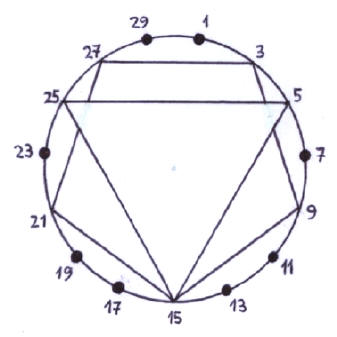
El reloj
Fig. 2. En los vértices de los polígonos regulares no puede haber primos.
Otro intento de asociar la distribución de los primos a figuras geométricas es utilizar la aritmética del reloj: Pensemos ahora en un cilindro imaginario de longitud infinita. Enrosquemos la recta numérica sobre su cara lateral haciendo que cada vuelta sea de 30 números. Marquemos con un punto únicamente los números impares. Ahora dibujemos un triángulo y un pentágono inscriptos en la base circular teniendo en cuenta que sus vértices coincidan con el número 15. Los números mayores que 10 encolumnados en los vértices del triángulo no pueden ser primos porque son divisibles por 5. Los encolumnados en los vértices del pentágono tampoco pueden ser primos porque son divisibles por 3. La figura se corresponde con la criba de 30 columnas.
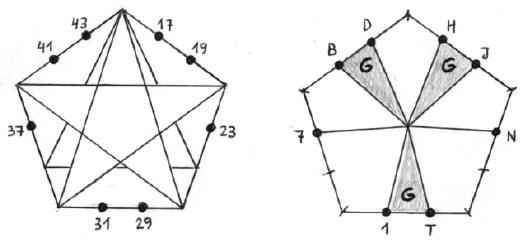
El pentágono
Pensemos ahora en un prisma imaginario de longitud infinita cuya base sea un pentágono. Enrosquemos la recta numérica sobre sus caras laterales, haciendo que cada vuelta sea de 30 números y teniendo en cuenta que el número 3 se ubique en una de las aristas longitudinales del prisma. Si ahora observamos la base pentagonal del prisma notaremos que los primos gemelos aparecen encolumnados en 3 de sus lados, 2 de los cuales son contiguos.
Fig. 3. Los primos gemelos sólo aparecen en 3 lados del pentágono.
Modelos insuficientes
La criba de 30 columnas, el reloj y el pentágono parecen revelar la existencia de cierto orden subyacente, pero en forma muy difusa. Sin embargo, las formas sencillas y regulares de estos modelos no dejan aflorar el patrón geométrico verdadero, que tiene una mayor complejidad. En este sentido decimos que son modelos insuficientes
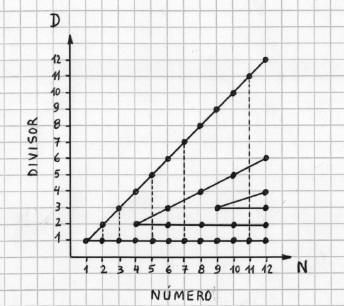
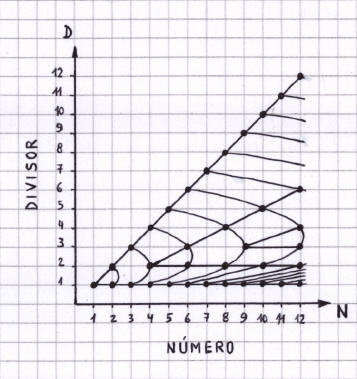
La determinación geométrica exacta de los números primos se logra sólo si se tiene en cuenta la estructura de divisores de los números naturales. La serie de la cantidad de divisores de los números naturales es tan o más irregular que la de los números primos y comienza con: 1, 2, 2, 3, 2, 4, 2, 4, 3, 4, 2, 6,... Esta estructura se pone de manifiesto en el modelo de curvas periódicas superpuestas y en el diagrama Número/Divisor que se muestran a continuación.
El modelo de curvas periódicas superpuestas
La serie de la cantidad de divisores de los números naturales y la serie de los números primos se determinan en forma geométrica de la siguiente manera: Desde elorigen de la recta numérica se traza una curva periódica por cada número natural. Cada curva debe interceptar al número natural y a sus múltiplos. Finalmente se remarca con un punto grueso a los números que han sido interceptados sólo por 2 curvas: Estos son los números primos.
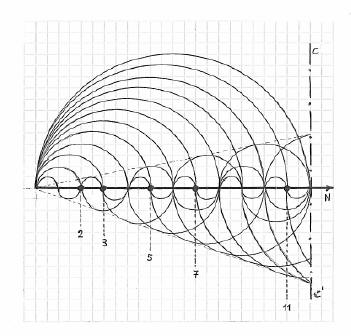Fig. 4. Los números primos son los únicos interceptados por 2 curvas.
Las Propiedades del modelo son:
La cantidad de divisores de cada número natural es igual a la cantidad de curvas que lo interceptan sobre la recta numérica. Por ejemplo: el 6 aparece interceptado por 4 curvas, por lo tanto tiene 4 divisores. Los números primos son los números que aparecen interceptados por 2 curvas. Por ejemplo: 2, 3, 5, 7, 11... Los números compuestos son los que aparecen interceptados por más de 2 curvas. Por ejemplo: 4, 6, 8, 9, 10, 12... Los números cuadrados son aquellos interceptados por una cantidad impar de curvas. Por ejemplo: 1, 4, 9,... Las lagunas son los segmentos de la recta numérica donde los números naturales son interceptados por más de 2 curvas. Por ejemplo; una pequeña laguna está localizada en el intervalo que contiene a los números 8, 9 y 10 (Véase la figura 4). Los divisores de cada número natural se corresponden con los semi-períodos de las curvas que lo interceptan. Por ejemplo: Las curvas que interceptan al número 6 tienen semi-períodos: 1, 2, 3 y 6. Por lo tanto los divisores de 6 son: 1, 2, 3 y 6. La construcción del diagrama se realizar con regla y compás o sino, utilizando gráficas de funciones periódicas. Por ejemplo: la gráfica de la función trigonométrica seno. La forma de la curva no es relevante sino los puntos en donde intercepta a la recta numérica. El tamaño del modelo puede extenderse trasladando el límite arbitrario CC´ hacia la derecha hasta donde se desee. El diagrama se va haciendo cada vez más complejo pero no tiene un límite teórico: Es infinito.
La fuente de divisores
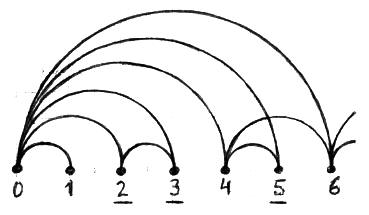Fig. 5. De cada número “brotan” sus divisores.
Con este nombre metafórico llamaremos a esta figura que se obtiene del modelo principal anulando las curvas que se encuentren debajo de la recta numérica. Se verá entonces salir o “brotar”, de cada número, una cantidad de líneas igual a la cantidad de divisores o factores del número. Por ejemplo: De los números primos 2, 3 y 5 “brotan” 2 divisores de cada número. Del número 4 “brotan” 3 divisores, etc.
Las parejas de factores
Fig. 6. Los factores se organizan en parejas.
En un contexto de multiplicación a los divisores también se los puede llamar factores.
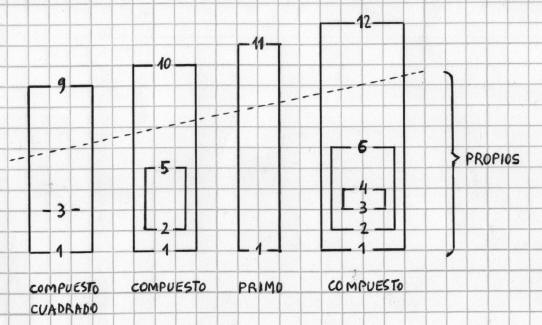
Los factores se organizan en parejas cuyo producto es igual al número. Los números cuadrados se distinguen porque siempre tienen un divisor central igual a la raíz cuadrada del número. Los divisores menores al número se llaman divisores propios o partes del número. Si la suma de divisores propios es mayor al número entonces se dice que el número es abundante. Si la suma es menor al número entonces se dice que el número es deficiente. Si la suma es igual al número entonces el número es perfecto.
El diagrama Número / Divisor
Fig. 7. Los números primos no tienen factores intermedios.
En este diagrama los divisores de cada número natural aparecen remarcados con un punto grueso sobre la vertical del número. Los números primos están determinados en forma geométrica al ser los únicos números que no presentan divisores intermedios entre sí mismos y la unidad. Esta característica aparece en el diagrama como una línea de trazos entre los divisores externos. La línea no es interceptada por ningún otro divisor en la vertical de cada primo. Se observa además que sobre la vertical de un número, los divisores que aparecen sobre el perímetro del mismo sector triangular forman parejas de divisores complementarios. Estos son los factores que al ser multiplicados entre sí dan como resultado el número original. Una variante opcional del dibujo consiste en trazar una línea que conecte los divisores o factores centrales de cada número. Otra opción es considerar la línea dibujada a 45º como si fuera la recta numérica Nótese que el diagrama también determina la ubicación de losnúmeros cuadrados ( 1, 4, 9, 16, 25, etc.). Estos son los únicos números naturales que tienen una cantidad impar de divisores. Los números cuadrados se distinguen porque su divisor central aparece en los vértices de los triángulos del diagrama. Si se traza una línea que una los vértices de los triángulos, entonces el diagrama queda dividido en 2 partes, siendo que cualquiera de ellas es suficiente para la determinación de los números primos. Una versión simplificada del diagrama, válida únicamente para números impares, se logra al omitir los triángulos en cuyo vértice se haya una raíz cuadrada par.
La red de factores
Fig. 8. Los factores forman una red.
Partiendo del diagrama Número / Divisor se puede construir una red de factores al trazar curvas que los relacionan. Por cada número natural hay una curva. Las curvas están dispuestas de manera tal que la línea imaginaria que une las raíces de 2 cuadrados siempre es interceptada sólo por una curva. La cantidad de factores contenidos en cada curva es igual al número de orden de la curva, siendo la primera de ellas la correspondiente al número 1, formada sólo por un punto. Este grafopermite lograr la factorización relativa de un número.
Factorización relativa
Llamamos aquí factorización relativa al proceso de encontrar los factores de un número sin operar directamente sobre él. La idea consiste en tomar el grafo anterior (Fig. 8) y tratar de reproducir la red de aristas y vértices o factores cercanos al número y con ello obtener los factores del número propiamente dicho. Debido a que es predecible la distancia entre los vértices adyacentes este proceso también puede lograrse utilizando solamente operaciones de suma y resta, prescindiendo de cualquier otra.
El modelo 3D
El modelo de curvas periódicas superpuestas y el diagrama Número / Divisor se relacionan entre sí pues son partes de un modelo mayor que tiene una estructuratridimensional. En el modelo 3D las curvas periódicas no se encuentran sobre el mismo plano, sino que cada curva se halla ubicada en un plano paralelo a los demás. Estos planos están separados entre sí por la unidad. A su vez la recta numérica se encuentra en un plano perpendicular a los planos que contienen las curvas. Los 2 diagramas mencionados al principio son sólo 2 vistas de este objeto tridimensional. Los puntos remarcados que se observan en el diagrama Número/Divisor son los puntos en donde las curvas interceptan en forma periódica al plano numérico, situado en forma perpendicular a ellas. Entonces el diagrama Número / Divisor contiene la parte esencial del modelo de curvas periódicas superpuestas.
El cometa
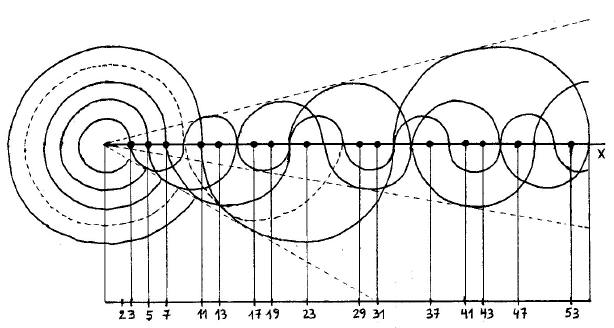Fig. 9. El cometa utiliza menos líneas para determinar los números primos.
El cometa es un modelo ha sido arreglado con círculos concéntricos para hacerlo más mnemotécnico. Su forma recuerda a los objetos astronómicos conocidos desde la antigüedad. La figura está formada por curvas periódicas que tienen una amplitud máxima en el origen de la recta numérica. Cada curva intercepta a un número y a todos sus múltiplos impares. La figura se puede trazar con regla y compás, o sino, utilizando la gráfica de otra función periódica, por ejemplo; la gráfica de la función trigonométrica coseno. Los números pares no se tienen en cuenta. Los curvas correspondientes a los números compuestos impares son opcionales. En este modelo noaparecen todos los divisores de los números naturales. El modelo utiliza una menor cantidad de líneas para determinar los números primos. Se destaca en forma especial la ubicación de los primos gemelos.
En la figura se distinguen 2 zonas: En la cabeza del cometa los números primos mayores a 2 aparecen interceptados únicamente por una curva, mientras que en la coladel cometa los primos son los números que no son interceptados. El diagrama es eficaz en la determinación de primos y compuestos hasta el número anterior al cuadrado del número primo siguiente al último número dibujado dentro de la cabeza. Por ejemplo el diagrama dibujado arriba es eficaz hasta el número 168 = (13 .13) –1. Para prolongar su eficacia hay que agregarle más curvas. El modelo puede tener una extensión infinita.
El sombrero
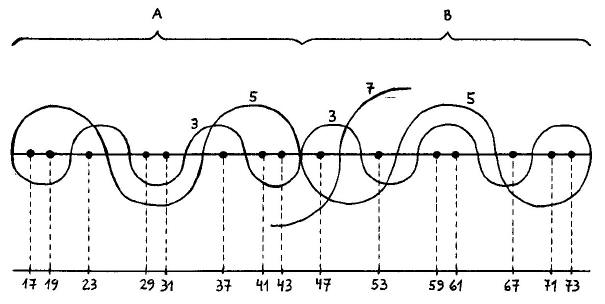Fig. 10. Los primos gemelos se alojan en la copa y en las alas del sombrero.
El sombrero es una figura que aparece dentro de la cola del cometa y que se repite una y otra vez en forma periódica. La figura está formada por curvas que representan a los divisores 3 y 5. Las curvas interceptan a los múltiplos impares de esos números. La figura se presenta, al derecho (B) y al revés (A), cada 30 números. Esta figura es interesante pues determina la ubicación de las parejas de primos gemelos. Los primos gemelos solo pueden alojarse en la copa o en las alas del sombrero. Vemos entonces que la figura puede contener como máximo 8 números primos: 6 de ellos formando 3 parejas de gemelos, más 2 primos solitarios.
Construcción de funciones
La gráfica de la función trigonométrica seno se representa como una onda periódica que intercepta una y otra vez a la recta numérica. Ahora decimos que un número (a) es divisible por otro (b) si el seno de (180 grados . a / b) es igual a cero. Utilizando esta afirmación adecuamos la función seno para que intercepte al número primo 2 y a todos sus múltiplos sobre la recta numérica.
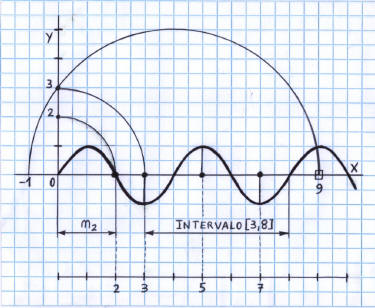Fig. 11. La función periódica determina números primos en el intervalo [3,8]
180º x
f(x) = A . sen -----------
2
|
El factor designado con la letra A es un coeficiente de amplitud que sirve para regular la altura de la curva con respecto a la recta numérica. Al dibujar la gráfica de esta función vemos que la curva es útil para determinar los números primos y los compuestos en el intervalo [3,8]: La curva tiene amplitudes en los números primos 3, 5 y 7 e interceptos en los números compuestos 4, 6 y 8. Fuera de ese intervalo la curva no es eficaz.
Si ahora se superpone al dibujo anterior una gráfica que intercepte al número 3 y a todos sus múltiplos, se obtiene la siguiente figura:
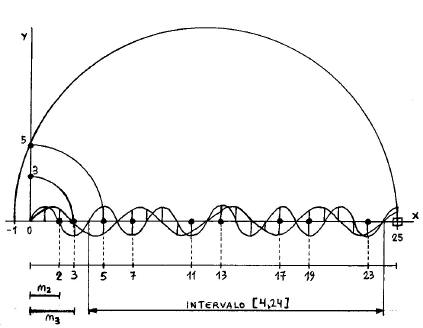Fig. 12. Las 2 funciones superpuestas determinan primos en el intervalo [4,24]
En el intervalo [4,24] las 2 curvas presentan amplitudes en los números primos 5, 7, 11, 13, 17, 19 y 23, mientras que en los números compuestos 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22 y 24 por lo menos una de las curvas intercepta al número. Esto permite identificar a primos y compuestos. La gráfica sólo es eficaz en el intervalo [4,24]. El límite inferior del intervalo es el número compuesto siguiente al mayor primo utilizado en las fórmulas. El límite superior es el número anterior al cuadrado del siguiente primo. Por ejemplo: El número 4 es el compuesto siguiente al número primo 3 y el número 24 es el compuesto anterior al cuadrado del número primo 5.
Ahora se multiplica las funciones que generaron las 2 curvas vistas arriba y se obtiene una función sencilla que permite dibujar una curva unificada:
| 180º x | 180º x | ||
| f(x) = A . sen | ------------ | . A . sen | ------------ |
| 2 | 3 |
La nueva función se representa con una curva que muestra amplitudes para los números primos e interceptos para los números compuestos en el intervalo [4,24].
Puede aumentarse las amplitudes de la curva aumentando el valor del coeficiente de amplitud (A). También se puede asignar un valor general al coeficiente, o sino, asignar un valor individual para cada componente de la serie de productos. Al coeficiente de amplitud se le asigna un valor constante o variable (Por ejemplo n / 2) según sea conveniente en la representación de la función.
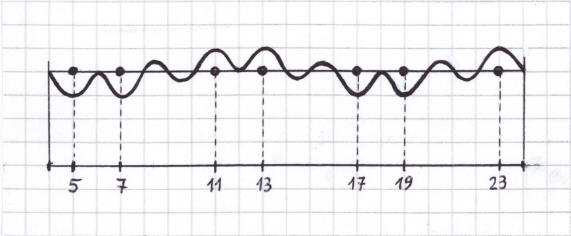Fig. 13. La función de los números primos en el intervalo [4, 24]
También puede utilizarse la función coseno a partir del segundo término de la serie con la salvedad que el denominador de cada término debe ser el doble del usado para la función seno.
Si ahora se aumenta la serie de productos de la función agregando el término relacionado con el tercer número primo (El 5) entonces se obtiene una gráfica con amplitudes para los primos e interceptos para los números compuestos en el intervalo [6,48].
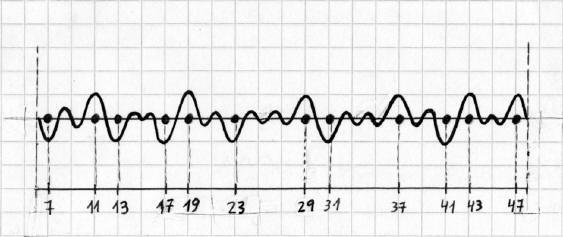Fig. 14. Se extiende la eficacia de la función en el intervalo [6, 48]
A medida que agregamos términos a la fórmula se pierde un poco de eficacia por el lado izquierdo de la recta numérica pero se compensa en demasía al ganar mucho más por el lado derecho de dicha recta.
Finalmente, si ahora se eleva al cuadrado la función anterior entonces se obtiene una gráfica que muestra picos para los números primos y líneas prácticamente rectas para los números compuestos. Obsérvese como, bajo la apariencia irregular y asimétrica de la gráfica, subyacen dos simetrías superpuestas centradas respectivamente en los números 15 y 30.
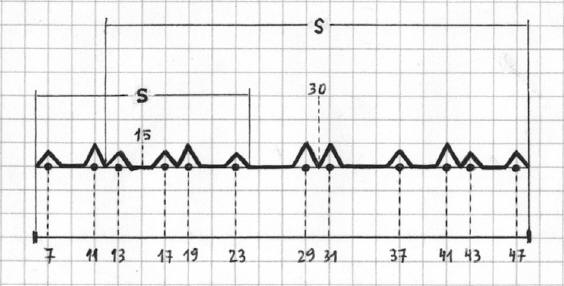Fig. 15. Gráfica de la función obtenida elevando al cuadrado la función anterior.
Los primos de Mersenne
Los primos de Mersenne son los números primos que anteceden a una potencia de 2 cuyo exponente es un número primo. En la recta numérica no es fácil encontrar esta clase de números porque no todas las potencias de 2 con exponente primo son precedidas por un número primo. Entre los primeros cien mil números sólo se encuentran 5 primos de Mersenne. Estos primos son importantes para la obtención de los números perfectos. La determinación geométrica de los primos de Mersenne se verá más adelante, en el modelo tríptico.
La serie de éstos primos comienza con: 3, 7, 31, 127, 8191, 131071,...
Los números triangulares
Son el resultado de sumar los números naturales: La serie comienza con: 1, 3, 6, 10,...
1 = 1
1 + 2 = 3
1 + 2 + 3 = 6
1 + 2 + 3 + 4 = 10
1 + 2 + 3 + 4 + 5 = 15
1 + 2 + 3 + 4 + 5 + 6 = 21
1 + 2 + 3 + 4 + 5 + 6 + 7 = 28
La serie de números triangulares puede representarse como la serie de vértices de una espiral numérica cuadrada, como se verá más adelante, en el modelo tríptico.
Los números perfectos
Los números perfectos tienen la particularidad de ser iguales a la suma de sus divisores propios. Por ejemplo, 28 es perfecto porque 1 + 2 + 4 + 7 + 14 = 28. Entre los primeros 30 millones de números sólo se encuentran 4 números perfectos. La serie de estas rarezas numéricas comienza con: 6, 28, 496, 8128, 33550336, 8589869056...
Los números perfectos equivalen a la mitad del producto entre un primo de Mersenne y el número que le sigue, es decir, una potencia de 2 con exponente primo.
Algunos ejemplos de obtención de números perfectos son:
| 3 x 4 | / 2 = | 12 / 2 = | 6 | |
| 7 x 8 | / 2 = | 56 / 2 = | 28 | |
| 31 x 32 | / 2 = | 992 / 2 = | 496 | |
| 127 x 128 | / 2 = | 16256 / 2 = | 8128 | |
| 8191 x 8192 | / 2 = | 67100672 / 2 = | 33550336 | |
| 131071 x 131072 | / 2 = | 17179738112 / 2 = | 8589869056 |
Los números perfectos también son números triangulares. Obsérvese que para los números perfectos el último de los sumandos es un primo de Mersenne:
1 + 2 + 3 = 6
1 + 2 + 3 + 4 + 5 + 6 + 7 = 28
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 +......+ 31 = 496
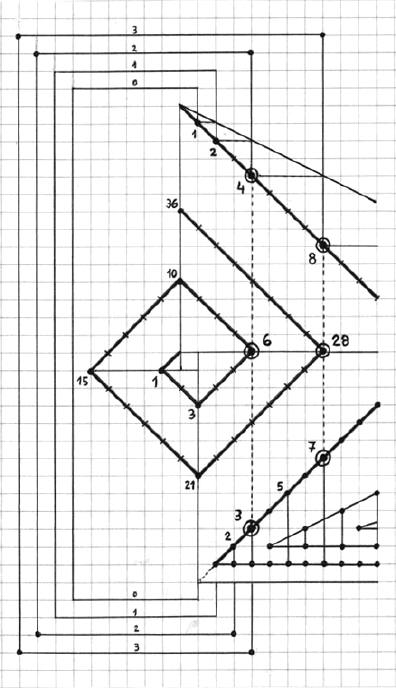
El tríptico
En cuanto a la distribución de los números perfectos, el patrón resultante se obtiene cuando se logra relacionar 3 modelos distintos (Véase la figura 16). En la parte superior del diagrama aparece el patrón de las potencias de 2. En el centro de la figura aparece una espiral numérica en cuyos vértices se encuentran los números triangulares. Abajo a la derecha aparece el diagrama Número / Divisor que permite la determinación geométrica de los números primos. Al relacionar el patrón de potencias de 2 y el patrón de los primos quedan determinadas las potencias de 2 con exponente primo y los primos de Mersenne. Finalmente relacionando estos 2 tipos de números con los números triangulares se determina la ubicación de los números perfectos.
Se observa en la espiral numérica que la distancia entre un número perfecto y el número triangular precedente es igual al primo de Mersenne. Por ejemplo 28 – 21 = 7. A su vez, la distancia entre el número perfecto y el número triangular siguiente es igual a la potencia de 2 con exponente primo . Por ejemplo: 36 – 28 = 8.
En la espiral aparecen los números perfectos 6 y 28 ubicados en los vértices de la primera y segunda vuelta, sobre el eje que apunta hacia el Este. El número de vuelta en donde aparece el número perfecto es la cuarta parte de la potencia de 2 asociada, es decir, es una potencia de 2 con un exponente 2 unidades menor que la otra. Por lo tanto, si se continúa dibujando la espiral, junto con los otros 2 patrones, el tercer número perfecto aparecerá en la vuelta 8, el cuarto número aparecerá en la vuelta 32, el quinto en la vuelta 2048, el sexto en la vuelta 32768 y así se irán encontrando, poco a poco, estas joyas de la matemática.
Fig.16. En la figura aparecen determinados: Las potencias de 2, los números primos,
los números triangulares, los cuadrados, las potencias de 2 con exponente primo, los primos de
Mersenne y los números perfectos.
los números triangulares, los cuadrados, las potencias de 2 con exponente primo, los primos de
Mersenne y los números perfectos.
Existe una relación entre las espirales numéricas y ciertos polinomios: Una cantidad infinita de rectas cruzan la espiral en diversas zonas, a distintas latitudes y longitudes y con diversos ángulos, siendo determinados los puntos que pertenecen en común a la espiral y a dichas rectas con este tipo de fórmulas. Por ejemplo, si designamos con la letra x el número de vuelta de la espiral, entonces la serie de números triangulares que se encuentran sobre cualquiera de los ejes, se calcula de la siguiente manera:
Sobre el eje Oeste el número triangular es: T = 8 x.x – 10 x + 3. Sobre el eje Sur es:
T = 8 x.x – 6 x + 1. Sobre el eje Este, donde se ubican los números perfectos, es:
T = 8 x.x – 2 x. Finalmente sobre el eje Norte es: T = 8 x.x + 2 x.
Nótese que los números triangulares que están sobre los ejes Oeste y Sur terminan en 1, 3 ó 5 y los que están sobre los ejes Este y Norte terminan en 0, 6 ú 8.
Las líneas periféricas que conectan al patrón de números primos con el patrón de las potencias de 2 tienen la misión de identificar el tipo de exponente de las potencias.Los exponentes de las potencias de 2 están representados entonces por éstas líneas. Las líneas cuyas esquinas están remarcadas con un punto identifican a los exponentes primos.
Obsérvese que el patrón de las potencias de 2 está alineado en su inicio con el eje Norte de la espiral, mientras que el patrón de los números primos está alineado en su inicio con el eje Sur. Por lo tanto hay un desfasaje de una unidad entre el patrón superior y el inferior. Cuando se encuentran alineados en la misma vertical; una potencia de 2 con exponente primo, un número triangular y un número primo entonces se determina geométricamente que éste último es un primo de Mersenne y el número triangular es un número perfecto.
Conclusión
La distribución de los números primos y de los números perfectos es perfectamente entendible con los modelos visuales que se vieron aquí. Los modelos geométricos que permiten determinar la posición de los números primos son los que tienen en cuenta la estructura de divisores de los números naturales. El modelo principal es un modelo de curvas periódicas superpuestas. Cada curva periódica representa un divisor. Las irregularidades en la distribución de los primos y las lagunas, o zonas desérticas, son el resultado de la complejidad que origina la superposición de infinitas curvas periódicas, especialmente cuanto más se sumergen en las profundidades de la recta numérica.
En cuanto a los números perfectos, son 3 patrones los que deben relacionarse para llegar a percibir visualmente las razones de su ubicación entre los demás números naturales.
Se concluye que, si bien todavía quedan grandes problemas a resolver sobre los números primos y perfectos, el tema de su determinación y representación geométrica no debería considerarse uno de ellos.
Omar Evaristo Pol2001-2007 - Todos los derechos reservados.
Hecho el depósito que marca la ley 11723.
Buenos Aires, Argentina.
|
TOMADO DE:http://www.polprimos.com/
Suscribirse a:
Entradas (Atom)