De antiguo es conocido el triángulo pitagórico: 3 2 + 4 2 = 5 2 Para algunos resultarán una sorpresa las siguientes generalizaciones de esa igualdad cuadrática: 10 2 + 11 2 + 12 2 = 13 2 + 14 2 = 365 21 2 + 22 2 + 23 2 + 24 2 = 25 2 + 26 2 + 27 2 Es inevitable preguntarse si estas igualdades son casuales u obedecen a alguna ley. ¿Es así?
SOLUCIÓN:
Si existe una ley, la correspondiente ecuación tomará la forma:
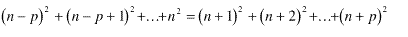
Desarrollando y simplificando se llega a:
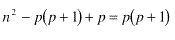
O sea, finalmente:
n = 2p(p + 1)De donde salen fácilmente los siguientes términos:
36
2 + 37
2 + 38
2 + 39
2 + 40
2 = 41
2 + 42
2 + 43
2 + 44
255
2 + 56
2 + 57
2 + 58
2 + 59
2 + 60
2 = 61
2 + 62
2 + 63
2 + 64
2 + 65
2Obsérvese que la base del último cuadrado del término de la izquierda es siempre el
cuádruple de un número triangular.
Estas series presentan una analogía trivial con las del tipo:
1 + 2 = 3
4 + 5 + 6 = 7 + 8
9 + 10 + 11 + 12 = 13 + 14 + 15
que es también muy fácil generalizar.
TOMADO DE:http://www.mensa.es/juegosmensa/s151155.html#SOLU152
