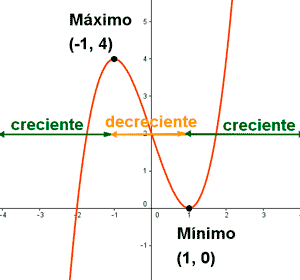
Máximos y mínimos de una función
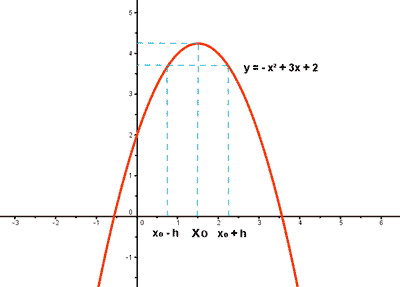
Máximo relativo de una función
Una función f alcanza un máximo relativo
en un punto de abscisa x0 si existe un entorno reducido de x0 ,
es decir E*(x0 , h) = (x0 - h, x0 + h) - { x0 } , tal que f(x) < f(x0)
para todos los puntos de dicho entorno reducido.
en un punto de abscisa x0 si existe un entorno reducido de x0 ,
es decir E*(x0 , h) = (x0 - h, x0 + h) - { x0 } , tal que f(x) < f(x0)
para todos los puntos de dicho entorno reducido.
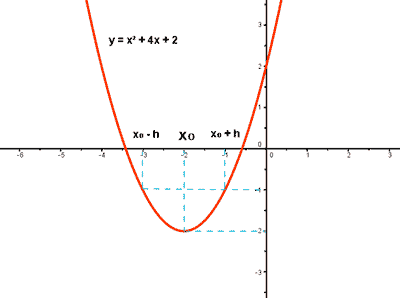
Mínimo relativo de una función
Una función f alcanza un mínimo relativo en un punto de abscisa x0
si existe un entorno reducido de x0 , es decir
E*(x0 , h) = (x0 - h, x0 + h) - { x0 } ,
tal que f(x) > f(x0) para todos los puntos de dicho entorno reducido.
si existe un entorno reducido de x0 , es decir
E*(x0 , h) = (x0 - h, x0 + h) - { x0 } ,
tal que f(x) > f(x0) para todos los puntos de dicho entorno reducido.
Entorno reducido: E*(x0 , h) = E(x0 , h) - { x0 } = ( x0 - h, x0 ) ∪ ( x0 , x0 + h )
Ejemplo de mínimos y máximos relativos de una función
Determinar los mínimos y máximos relativos
en la gráfica de la siguiente función:
f(x) = x3 - 3x + 2
• El punto (-1 , 4) es un máximo relativo.
• El punto (1 , 0) es un mínimo relativo.
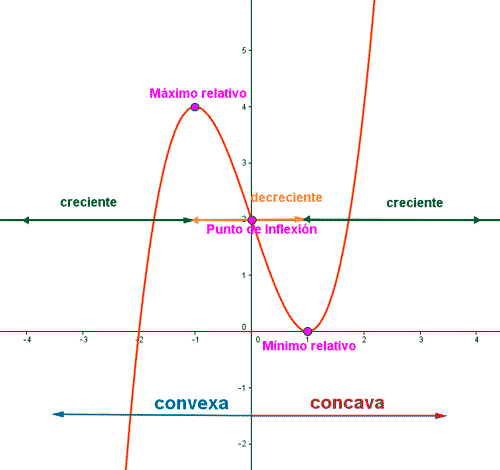
Máximos y mínimos relativos
Una función f(x) tiene un máximo relativo en x = c si f(a) ≥ f(x) para todo x en algún entorno del punto a .
Una función f(x) tiene un mínimo relativo en x = a si f(a) ≤ f(x) para todo x en algún entorno del punto a .
Criterio de la primera derivada
En un punto crítico x = a , una función derivable f(x) tiene:
• un máximo relativo si f ' (x) cambia de positiva a negativa (↑↓)
• un mínimo relativo si f ' (x) cambia de positiva a negativa (↓↑)
• no tiene máximo ni mínimo relativo si f ' (x)
no cambia de signo (↑↑ o ↓↓)
no cambia de signo (↑↑ o ↓↓)
Criterio de la segunda derivada
En un punto crítico x = a , una función derivable f(x) tiene:
• un máximo relativo si f '' (a) < 0
• un mínimo relativo si f '' (a) > 0
La condición necesaria para que una función tenga un máximo relativo es que su primera derivada en ese punto sea igual a 0 y la condición suficiente es que su segunda derivada en ese punto sea menor que 0.
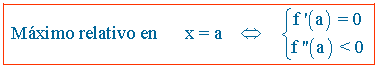
La condición necesaria para que una función tenga un mínimo relativo es que su primera derivada en ese punto sea igual a 0 y la condición suficiente es que su segunda derivada en ese punto sea mayor que 0.
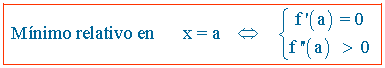
Procedimiento para hallar los máximos y mínimos relativos
Estudia los máximos y mínimos relativos de la siguiente función: f(x) = x3 - 3x + 2
1) Se calcula la primera derivada: f ' (x)
Calculamos la primera derivada de la función.
f ' (x) = 3x2 - 3
2) Se resuelve la ecuación: f ' (x) = 0
A continuación calculamos las raíces de la primera derivada.
3x2 - 3 = 0 ⇔ 3x2 = 3 ⇔ x2 = 1 ⇔ x = ±1
Por lo tanto la primera derivada se anula en x = -1 y x = 1 .
3) Se sustituyen las raíces de f ' (x) = 0 en la función inicial y se obtienen los posibles máximos y mínimos relativos.
• f (-1) = 4 ⇒ El punto (-1, 4) es un posible máximo o mínimo relativo
• f (+1) = 0 ⇒ El punto (+1, 0) es un posible máximo o mínimo relativo
4) Se calcula la segunda derivada: f '' (x)
Calculamos la segunda derivada.
f '' (x) = 6x
5) Se sustituyen la abscisa de los posibles máximos y mínimos relativos en la segunda derivada f '' (x)
• Si f '' (x) < 0 es un máximo relativo
• Si f '' (x) > 0 es un mínimo relativo
En nuestro caso tenemos que:
• f '' (-1) = - 6 < 0 ⇒ (-1, 4) es un máximo relativo
• f '' (+1) = 6 > 0 ⇒ (+1, 0) es un mínimo relativo