| M | I | L | |||||
| + | M | I | L | ||||
| _ | _ | _ | _ | _ | _ | _ | _ |
| ? | ? | ? | ? | ? | ? | ? |
Los símbolos son: M M X C V I I I .
La suma está expresada en numeración romana. Así:
Entre los bloqueos conceptuales se encuentra el de falso hecho admitido, por ello para la resolución de problemas no hay nunca que dar por sentado más que lo que específicamente se exprese en el enunciado. En este caso, admitir sin más, que los símbolos expresan dígitos, cierra el camino hacia la solución.
La suma está expresada en numeración romana. Así:
| M | I | L | 1 | 0 | 4 | 9 | ||||||||||||||
| + | M | I | L | + | 1 | 0 | 4 | 9 | ||||||||||||
| _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | ||||||||
| M | M | X | C | V | I | I | I | 2 | 0 | 9 | 8 |
Entre los bloqueos conceptuales se encuentra el de falso hecho admitido, por ello para la resolución de problemas no hay nunca que dar por sentado más que lo que específicamente se exprese en el enunciado. En este caso, admitir sin más, que los símbolos expresan dígitos, cierra el camino hacia la solución.
2) Determinar la probabilidad de que en un sorteo de Lotería Primitiva aparezcan al menos dos números consecutivos cualesquiera.
SOLUCIÓN
La solución más sencilla pasa por calcular el número de combinaciones en las que no hay números consecutivos y restarlo luego del total.
Consideremos los dos conjuntos siguientes:
C1 = Combinaciones de 6 números del 1 al 49 tales que entre ellos no hay dos consecutivos.
C2 = Combinaciones cualesquiera de números del 1 al 44.
Ambos conjuntos tienen igual número de elementos, dado que existe entre ellos la siguiente correspondencia biunívoca: (a,b,c,d,e,f) <-> (a,b-1,c-2,d-3,e-4,f-5)
dónde a,b,c,d,e,f son números entre 1 y 49 tales que no hay entre ellos dos consecutivos. Por ejemplo, la combinación (1,5,7,20,35,49) de C1 se correspondería con la (1,4,5,17,31,44) de C2. El número de C2 es el combinacional de 44 sobre 6 = 7.059.052. Puesto que C1 y C2 tienen el mismo número de elementos Card(C1)=Card(C2)=7.059.052.
La cantidad total de combinaciones de la Lotería Primitiva es el combinacional de 49 sobre 6 = 13.983.816.
Luego, el número de tales combinaciones en las que no hay dos elementos consecutivos es la diferencia: 13.983.816 - 7.059.052 = 6.924.764
La probabilidad de que salgan dos números consecutivos cualesquiera en un sorteo es, en consecuencia 49,52%.
Consideremos los dos conjuntos siguientes:
C1 = Combinaciones de 6 números del 1 al 49 tales que entre ellos no hay dos consecutivos.
C2 = Combinaciones cualesquiera de números del 1 al 44.
Ambos conjuntos tienen igual número de elementos, dado que existe entre ellos la siguiente correspondencia biunívoca: (a,b,c,d,e,f) <-> (a,b-1,c-2,d-3,e-4,f-5)
dónde a,b,c,d,e,f son números entre 1 y 49 tales que no hay entre ellos dos consecutivos. Por ejemplo, la combinación (1,5,7,20,35,49) de C1 se correspondería con la (1,4,5,17,31,44) de C2. El número de C2 es el combinacional de 44 sobre 6 = 7.059.052. Puesto que C1 y C2 tienen el mismo número de elementos Card(C1)=Card(C2)=7.059.052.
La cantidad total de combinaciones de la Lotería Primitiva es el combinacional de 49 sobre 6 = 13.983.816.
Luego, el número de tales combinaciones en las que no hay dos elementos consecutivos es la diferencia: 13.983.816 - 7.059.052 = 6.924.764
La probabilidad de que salgan dos números consecutivos cualesquiera en un sorteo es, en consecuencia 49,52%.
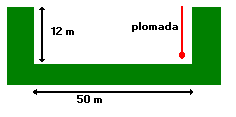
3) Mi empresa ejecuta una obra, de la que se ha completado la excavación. Esta consiste, aproximadamente, en un vaciado de planta cuadrada, con 50 m de lado y 12 m de profundidad. Conversando un día con un arquitecto compañero, se nos ocurrió si la plomada librada a lo largo de uno de los lados de la excavación se desviaría mucho de la vertical como consecuencia del vaciado.
¿Puede calcularlo el amable lector?. Tome la densidad del terreno igual a 2000 kg/m³ y recuerde que el radio de la tierra es 6730 km, y su masa, 6*1024 kg.
SOLUCIÓN
La aceleración de la gravedad g vale 9,81 m/s².
g = GM/R² = 9.81 m/s²siendo G la constante de gravitación universal, M la masa de la Tierra y R su radio.
El peso de un cuerpo en la superficie terrestre es la composición de las atracciones sobre él de todos los átomos de la Tierra, y equivale a la que ejercería la masa de ésta concentrada en su centro. El hueco de la excavación supone introducir en ese conjunto una asimetría substractiva, cuyo resultado neto es lógicamente una repulsión del mismo valor que la atracción gravitatoria que ejercería el volumen de tierras del hueco.
Se puede asimilar también ésta, bastante aproximadamente, a la que ejercería una masa equivalente contentrada en el centro de gravedad de la excavación, o sea:
g' = Gm'/r'²
m' = 50.50.12.2000 = 6.107 kg r' = (25² + 6²)½ = 25,71 m
g' 6.107.(6,37.106)² - = ------------------- g 6.1024.(25,71)² g'/g = 6,14*10-7
La componente horizontal de esa fuerza vale:
g'x /g = 6,14.10-7 (25/25,71) = 5,97 .10-7
x = 12.5,97.10-7 m = 7,16.10-6 m = 0,00716 mm
2x - 3y = 1
SOLUCIÓN
Puesto que la diferencia es positiva se cumple que x > y. Procediendo al cambio de variable x = a+y la expresión queda:2a+y - 3y = 1 => 2a 2y - 3y = 1 => 2a(10/5)y - 3y = 1 => 2 a 10 y = 15 y + 5 y (I)El primer miembro de (I) termina en "y" ceros. Vamos a ver en cuantos ceros termina el segundo miembro. Obtenemos las primeras potencias de 15 y 5. Si nos fijamos en las terminaciones vemos que:
y 15y 5y La suma 15y + 5y termina en "y" ceros 0 1 1 0 1 5 5 1 2 225 25 1 3 3375 125 2 4 50625 625 1 5 759375 3125 2
Cuando y>2 15ytermina 5ytermina La suma termina Impar 375 125 500 (2 ceros) Par 625 625 350 (1 cero) Es así porque 375 x 15 termina en 625 y 125 x 5 termina en 625 mientras que 625 x 15 termina en 375 y 625 x 5 en 125Luego la igualdad (I) no se cumple para y>2: Primer miembro 2 ceros, segundo miembro 1 cero (225+25=250). Como consecuencia, la ecuación planteada sólo puede cumplirse para y<=2, concretamente para (1,0) y (2,1).
TOMADO DE: http://www.mensa.es/juegosmensa/e001005.html#ENUN001
