CHISTE N° 26

TOMADO DE: http://elmejorhumorinteligente.blogspot.com/2011/08/atasco-matematico.html

Logaritmos: definición, propiedades y ejercicios resueltos

TOMADO DE: http://www.ejerciciosweb.com/logaritmos/ejercicios-resueltos.html

El Área y la Integral: Algo de Historia

Encontrar la tangente a una curva, y hallar el área limitada por una curva, han sido dos problemas geométricos tratados sistemáticamente a lo largo de la historia por el cálculo; ambos quedan resueltos por medio de un “paso al límite” y ambos como veremos están íntimamente ligados.

Por intuición sabemos todos lo que es un área, del mismo modo que creemos saber los significados de longitud, tiempo, velocidad, volumen…; somos también conscientes de que estamos utilizando estas palabras en dos sentidos: unas veces para significar una cantidad física y otras veces para significar una «medida» de dicha cantidad. Por ejemplo la palabra «área» significa un pedazo libre de terreno llano, pero para evitar circunloquios decimos el área es de 5 fanegas donde la palabra área quiere decir la medida del área. El uso y su significado queda por lo general claro a través del contexto.

Algo de Historia

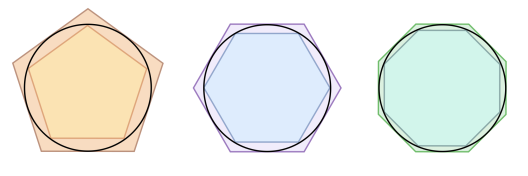
Las culturas babilonias y egipcias son ya precursoras de una incipiente geometría muy aritmetizada. En ambas culturas (los babilonios, parece ser, fueron mejores algebristas que los egipcios y peores geómetras) se relacionaba el área de una figura plana con su perímetro. Se conocían métodos correctos para obtener áreas de triángulos y rectángulos, y buenas aproximaciones a partir de la comparación con el cuadrado del pentágono, hexágono…(2200a.C).

El paso siguiente de obtener áreas de figuras planas limitadas por curvas específicas, tales como un arco parabólico, no se alcanzó aparentemente hasta los tiempos de Arquímedes (287-212 a.C.). Antes, Antifonte (430 a.C.) y Eudoxo (409-356 a.C.), como nos ha transmitido Euclides en sus Elementos, obtienen el área de un círculo mediante una sucesión de polígonos regulares inscritos y calculan volúmenes como los del cono, la pirámide…

ARQUÍMEDES Y EL MÉTODO DE EXHAUCIÓN

Se suele citar a Arquímedes como el precursor del cálculo integral. En su libro SOBRE LA CUADRATURA DE LA PARÁBOLA, nos presenta el conocido Método de Exhaución (Agotamiento); de un modo sencillo puede describirse así: dada una región cuya área deseamos determinar, se inscribe en ella una región poligonal que se aproxime a la dada, y cuya área sea conocida o de fácil cálculo. Luego se elige otra región poligonal que dé una aproximación mejor, continuándose el proceso tomando cada vez polígonos de mayor número de lados y que tiendan a llenar la región dada inicialmente.

Arquímedes utilizó el método exhaustivo para conseguir el valor aproximado del número π.

Una de sus comprobaciones elementales consistía en recortar la región en un material de densidad uniforme y comparar su peso con el de una forma poligonal del mismo material y de área conocida. Más allá del cálculo de algunas áreas limitadas por curvas, es el método (esencialmente el mismo que utiliza Cauchy y Riemann) el que lo hace precursor del cálculo integral. En él se deja entrever la construcción de una sucesión de valores, su convergencia y la unicidad del límite.

Arquímedes demostró que el área del segmento parabólico de la figura superior es igual a 4/3 de la del triángulo inscrito de la figura inferior.

EL SIGLO XVII

 En los diecinueve siglos que separan a Arquímedes de Cavalieri no se encuentran progresos esenciales en la vía abierta por el “Siracusano”. Buenaventura Cavalieri (1591? – 1647) es otro gran precursor del cálculo integral, y su Geometría Indivisíbilus Continuorum (1645) significa un progreso considerable en dirección distinta a la de Kepler. Mientras el gran astrónomo alemán persiste en la vía arquimediana de sumar los elementos infinitesimales en que se descompone cada figura, vano empeño casi siempre, el jesuita italiano evita la sumación directa y se limita a comparar dos figuras para deducir la extensión de una mediante la otra. Cada recinto plano lo considera como suma de infinitos segmentos paralelos, y cada cuerpo como suma de sus infinitas secciones paralelas. Tales segmentos y secciones planas son los llamados “indivisibles” de Cavalieri. No se sabe cuales fueran los indivisibles de Galileo, que también estaba en posesión de una teoría análoga, pues no llegó a publicar nada, pero en su obra “Discursi” (1638) efectúa una verdadera integración de la función g.t, para llegar a la ley de caída de los graves: ½.g.t2

Mientras que el método exhaustivo (agotamiento) utilizado por Arquímedes opera sobre las propias figuras, el método de los indivisibles sustituye a una figura dada por la suma de una infinidad de elementos que tienen una dimensión menos.

El tratado de los indivisibles de Cavalieri es oral y no muy claro. El autor no dice en ninguna parte de su obra qué entiende exactamente por el término «indivisible»  que caracteriza a los elementos infinitesimales utilizados en su método.

El resultado fundamental de la geometría de Cavalieri es su famoso principio (ver Nota 1): dos figuras planas o espaciales que tienen equivalentes sus secciones paralelas son equivalentes.

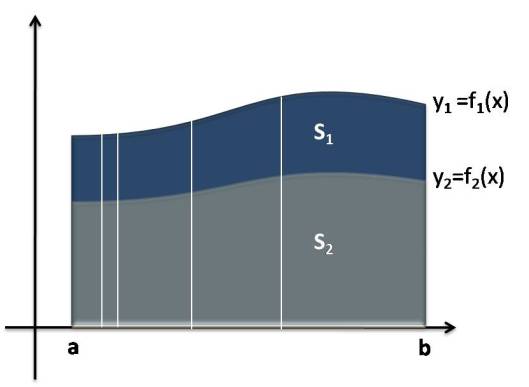
«Si dos áreas planas son tales que toda paralela a una dirección dada las corta, según segmentos cuyas longitudes están en una proporción constante, las áreas están en la misma razón» (Figura1)

Principio de Cavalieri: ambas torres de monedas tienen el mismo volumen, no importa la inclinación sino el área de cada sección y la altura total.

 Estas afirmaciones son prácticamente equivalentes a los razonamientos actuales del tipo: Se dan dos figuras limitadas por el eje OX, las rectas x=a, x=b y las curvas dadas por y1 =f1(x) , y2=f2(x). La relación entre las áreas, viene dada por:

Gran progreso estaba reservado al cálculo integral, por obra de Jhon Wallis (1616 – 1703), que abandona el método geométrico de los matemáticos continentales, abordando la integración aritméticamente; y para poner de manifiesto su designio, titula su obra Arithmetica Infinitorum (1655).

Mientras que Cavalieri había llegado al resultado: Estas afirmaciones son prácticamente equivalentes a los razonamientos actuales del tipo: Se dan dos figuras limitadas por el eje OX, las rectas x=a, x=b y las curvas dadas por y1=f1(x) , y2=f2(x). La relación entre las áreas, viene dada por:

Con este principio llega en 1647 a resultados que equivalen, con el tecnicismo actual, a calcular las integrales de las potencias xn de exponente natural. por medio de una laboriosa correspondencia entre indivisibles, Wallis abandona el marco geométrico y en su Arithmetica Infinitorum aritmetiza la Geometría Indivisibilibus de Cavalieri.

Básicamente su idea consiste en asociar valores numéricos a los infinitos indivisibles deCavalieri.

Para ilustrar el método de Wallis consideremos el problema de calcular el área bajo la curva   y= xk (k = 1, 2,. . . ) y sobre el segmento [0, a].

Siguiendo a Cavalieri, Wallis considera la región PQR formada por un número infinito de líneas verticales paralelas, cada una de ellas con longitud igual a xk.

Por tanto, si dividimos el segmento PQ = AB = a en n partes de longitud h = a/n, donde n es infinito, entonces la suma de estas infinitas líneas es del tipo

Análogamente, el área del rectángulo ABCD es:

La razón entre el área de la región PQR y el rectángulo ABCD es:

Esto lleva a Wallis a estudiar el valor de esta expresión para n infinito.

Después de estudiar varios casos para valores de k = 1, 2, 3 haciendo, en cada caso, sumas para distintos valores de n = 1, 2, 3, 4, por ejemplo para k=2, se tiene:

Wallis observa ciertas regularidades en las mismas y, con tan débil base, acaba afirmando que para n infinito y para todo k = 1, 2, . . . , se verifica que:

Naturalmente, de aquí deduce el valor del área de la región PQR

Este resultado ya era conocido anteriormente, pero Wallis no se paraba aquí y extendía la validez de la igualdad (6) a todos los exponentes racionales positivos. Su peculiar razonamiento tiene interés pues en él se basó Newton para obtener la serie binomial.

Junto a los antes mencionados Cavalieri y Wallis, merecen destacarse en el mismo orden matemáticos como Descartes (1596–1650), Pascal (1623–1662) y Fermat (1601–1665).

Barrow (1630–77), fue el primero que ideó la determinación de la tangente mediante el cociente de incrementos y quién en 1669 mostró mediante su regla que el problema de las tangentes se relaciona con el problema del área limitada por una curva, vinculándolo así con el cálculo integral, que evolucionaba desde tiempos más remotos por cauces muy distintos. Desde entonces ambos problemas se entrelazan y se complementan, por lo que su evolución histórica debe seguirse simultáneamente.

La importancia de la regla o resultado de Barrow no se puede ponderar suficientemente:

Para una función continua, si consideramos la Integral Definida como una función de su límite superior:

Entonces se demuestra que F es derivable y que además F´(x)=f(x). Representa la sencilla fórmula:

Nexo de unión, como sabemos, conocido como Teorema fundamental del Cálculo, que nos informa como la derivación deshace la integración y la integración deshace la derivación. Nace el concepto de Función Primitiva, herramienta para el cálculo de la integral definida, concepto que no podemos confundir con el propio de la integral definida. La integral definida la interpretamos como un área y la función primitiva será la herramienta natural para su cálculo.

El cálculo integral de Arquímedes, que se proponía la evaluación de áreas por artificios de sumación tan ingeniosos como infecundos y el cálculo diferencial, nacido en el siglo XVII, para la resolución del problema de la tangente, por obra de Fermat, Pascal, etc. Disciplinas ambas que parecían condenadas a la esterilidad, de cuya conjunción expresada por la fórmula anterior nació el Análisis Moderno, por obra de Leibnitz (1646–1665) y Newton (1642–1727), descubridores y responsables del desarrollo de las ideas básicas del cálculo integral. Su mayor logro fue relacionar el cálculo integral con el cálculo diferencial, inaugurando así una etapa de desarrollo sin precedentes de la matemática.

Siglos XIX y XX

En la segunda mitad del siglo XIX y principios de XX, la clarificación del concepto de integral hace estudiar con precisión el concepto de área con carácter general, y aclarar los dos problemas fundamentales: ¿Cómo se puede definir el área? ¿Tiene área cualquier región del plano? ¿Cómo puede calcularse el área de una región? Cauchy (1789 –1857), a principios del siglo XIX, Riemann (1826 –1866), a mediados del XIX y Lebesgue (1875 – 1941), a principios del XX, han sido los sucesivos constructores del cálculo integral, habiendo en este siglo extensiones muy importantes con las que se ha podido abordar problemas inaccesibles con las herramientas clásicas. Así, hablando grosso modo, la construcción de la integral definida.

debida a Cauchy nos proporciona un método para medir la región (Trapecio Mixtilíneo) asociada a una función real no negativa y continua en un intervalo compacto de R que puede resumirse en la siguiente idea:

Para hallar el área de una región limitada por la gráfica de una función positiva f definida en [a,b], se divide el intervalo [a,b] en un cierto número de subintervalos, por ejemplo «n», designando por Dxk la longitud del k-ésimo intervalo, se consideran las sumas de la forma:

en donde tk designa un cierto punto del intervalo k-ésimo Dxk . Una suma de este tipo es una aproximación mediante rectángulos del área que intentamos calcular.

Si f es una función con comportamiento suficientemente regular en [a,b] – por ejemplo continua- entonces cabe esperar que estas sumas tengan un límite cuando n se hace infinito, si hacemos las subdivisiones cada vez más finas.

La noción de Integral de Riemann ofrece un método para extender la noción anterior a funciones «más generales» eludiendo la hipótesis de continuidad dada en Cauchy y ampliándola a funciones acotadas no demasiado discontinuas. (ver nota 2).

Existe otra generalización de la Integral de Riemann, la conocida Integral de Lebesgue (ver Nota 3).

Puede decirse que la integral de Riemann

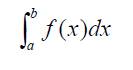
está bien construida, es fácil describirla y es útil a todas las necesidades del Cálculo elemental. Sin embargo, esta integral no cubre todas las necesidades del Cálculo superior.

Que las funciones muy discontinuas resulten no integrables es un primer inconveniente de la integral de Riemann, desde otra perspectiva la integral de Riemann posee un comportamiento anormal respecto a la operación del paso al límite, en el sentido que pueden encontrarse sucesiones de funciones integrables Riemann que convergen a una función no integrable Riemann.

El intento de Lebesgue de medir conjuntos arbitrarios de puntos de la Recta Real y de modelar un nuevo concepto de función para establecer el de función medible tiene su origen en los dos inconvenientes presentados anteriormente a la Integral de Riemann.

En un trabajo, ya clásico, -Integral, Longuer, Aire- publicado en 1902, Lebesgue da la definición de «medida» para un conjunto de puntos y lo aplica al desarrollo de esta nueva integral, estableciendo el concepto de medida de un conjunto como una fuerte generalización del concepto de longitud de un intervalo; La definición de medida que proporciona Lebesgue es la base de la definición de integral que lleva su nombre.

En su trabajo, Lebesgue, recurre a la Teoría de Conjuntos, a un nuevo concepto de función (Cantor-Borel) y a su Teoría de la medida para forjar su integral.

En la Integral de Lebesgue se cumplen un mayor número de Teoremas de convergencia.

Si una sucesión de funciones {fn } converge puntualmente hacia una función límite f en [a,b], sería deseable poder concluir que:

con un mínimo de hipótesis adicionales. El resultado definitivo en este sentido lo proporciona el «Teorema de convergencia dominada de Lebesgue». El teorema es falso para las integrales de Riemann.

Veamos dos ejemplos didácticos que ilustran la diferencia estratégica existente entre Rieman y Lebesgue:

a)    Si se tratara de medir el dinero que supone una gran cantidad de monedas dispuestas sobre una mesa, Riemann cuadricularía la mesa en rectángulos y contaría las monedas en cada uno de ellos; Lebesgue, en cambio, clasificaría las monedas y contaría después.

b)    Supongamos que queremos obtener el número medio de personas que hacen uso del metro en una estación determinada en el periodo de un mes. Riemann representaría esta situación gráficamente en un sistema de eje horizontal el tiempo y vertical el número de personas que hacen uso del metro en un instante determinado.

Riemann dividiría el eje de los tiempos en días y multiplicaría la fracción 1/30 (supuesto meses de 30 días) por uno de los valores del número de personas que entran en la estación un instante determinado de cada día sumando los resultados obtenidos para cada uno de los 30 días. Repetiría el procedimiento haciendo una subdivisión, ahora más fina dividiendo el eje de tiempos en horas, obteniendo un resultado más aproximado. Continuaría indefinidamente subdividiendo el eje tiempo en subintervalos cada vez más pequeños… (con longitudes tendientes a cero) observando que los valores obtenidos cada vez que subdivide tienden a un número fijo. Lebesgue, utilizaría otro procedimiento: en lugar de subdividir el eje de los tiempos, él subdivide el de las personas entre las ordenadas máximas y mínimas. Por ejemplo una subdivisión en decenas de personas; así, los valores del tiempo para los cuales la función que describe la situación está comprendida, por ejemplo entre 40 y 50 personas, determinan un conjunto de puntos que admite una medida «m» (en el sentido Lebesgue). Así, consideraría el producto de una ordenada cualquiera comprendida entre 40 y 50 por el número m/30. Sumaría a continuación todos los productos relativos a cada uno de los intervalos de la subdivisión en decenas de individuos y obtendría un número M´. Repetiría este proceso con subdivisiones cada vez más pequeñas (con longitudes tendientes a cero), obteniendo una serie de valores M´, M´´,M´´´…, que puede admitir un límite finito que sería el valor encontrado por Lebesgue. Mientras Riemann divide el intervalo de integración en subintervalos jerarquizados por el orden, Lebesgue, pudiera decirse que subdivide el intervalo en conjuntos medibles liberándose la jerarquización que le impone el orden. Desde este primer trabajo de Lebesgue, tanto la «Teoría de la Medida» como la Teoría de la Integración han sufrido muchas generalizaciones y modificaciones. Los trabajos de Young, Daniell, Riesz, Stone y otros, han probado que la Integral de Lebesgue puede introducirse de tal manera que no dependa de la Teoría de la Medida sino que esté orientada directamente a las funcionesy sus integrales. Es más, por medio de la integral de Lebesgue, es posible desarrollar la Teoría de la Medida.

 Apéndice

La medida del Conjunto Perfecto de Cantor

El conjunto perfecto de Cantor, también llamado conjunto ternario de Cantor, es un subconjunto del Intervalo real I=[0,1], que se construye mediante el siguiente proceso:

P1 es el Intervalo centrado en I de longitud 1/3

Para k=2,3, …., Pk es la unión de los intervalos abiertos de longitud 1/3k centrados en cada uno de los 2k-1 intervalos cuya unión es el complementario en I de:

Se designa por P la unión de todos los Pk. El conjunto C ternario de Cantor es: C=I-P.

Interesa también considerar, para cada k, el conjunto:

Veamos algunas propiedades del conjunto de

Cantor:

No es vacío pues contiene los extremos de los intervalos que conforman los Pk.

Es cerrado, pues P es abierto.

No contiene intervalos.

Es denso en sí mismo.

Tiene la potencia del continuo.

Nos podemos preguntar ahora ¿Qué medida tiene C?

En la construcción del conjunto P a partir del intervalo [ 0,1] , hemos comenzado eliminando un intervalo adyacente de longitud 1/3, después 2 intervalos adyacentes de longitud 1/9, luego 4 de longitud 1/27, etc. De forma general, en el paso n-ésimo habremos suprimido 2n-1 intervalos de longitud 1/ 3n. Así pues, la longitud de todos los intervalos suprimidos será:

siendo esta suma la de los términos de una progresión geométrica de razón 2/3 y cuyo primer término es 1/3.

Por tanto su suma vale:

así pues la suma de los intervalos adyacentes al conjunto de Cantor es 1. Dicho de otra forma, la medida del conjunto abierto P complementario de C es 1. Por tanto, la medida de C es m (C) = 1- m (P) = 1 –1 = 0. Este ejemplo demuestra que existen conjuntos con la cardinalidad del continuo, con la misma cardinalidad que R cuya medida es 0.

NOTAS

Nota 1. Una crítica al principio de Cavalieri: Los indivisibles de las líneas son puntos y estos no son operativos lo que con su método se impide la obtención de longitudes de curvas.

Nota 2. Teorema o Criterio de Lebesgue para la existencia de una Integral de Riemann:

«Sea f una función definida y acotada en un intervalo I=[a,b] de R, entonces f es integrable según Riemann si y sólo si, el conjunto de puntos de discontinuidad de f en I es de medida nula».

Nota 3. Una función NO integrable Riemann y SI integrable según Lebesgue.

Como ejemplo calculamos la integral de la función de Dirichlet en [0,1]:

Puesto que la medida del conjunto de los Irracionales es 1 en [0,1], entonces:

La integral de Riemann de esta función no existe.

TOMADO DE: http://euclides59.wordpress.com/2012/12/16/el-area-y-la-integral-algo-de-historia/