Published 04/04/2014
Aut.: M. Macho , Estadística , Historia , Matemáticas
La matemática es la ciencia que señala las conclusiones necesarias es una frase del matemático Benjamin Peirce (1809-1880), que hoy cumpliría 205 años.
Está contenida al principio de su libroLinear Associative Algebra (1872), y esta definición de matemática fue avalada por su hijo Charles Sanders Peirce como una ayuda para iniciar la filosofía del pragmatismo.
En estadística, Peirce propuso el llamado criterio de Peirce para el tratamiento estadístico de valores atípicos, siendo la teoría desarrollada posteriormente por su hijo.
Benjamin Peirce 's padres Lydia Cuerdas Nichols y Benjamin Peirce. Benjamin, el tema de esta biografía, por lo tanto tenía el mismo nombre que su padre, que era a la vez un legislador del estado de Massachusetts y también un bibliotecario de la Universidad de Harvard. Tomamos nota de que este apellido se pronuncia "Bolso". A pesar de Harvard había sido establecido para alrededor de 170 años en el momento del nacimiento de Benjamin, que todavía estaba bajo el control político bastante estrecho y no es una institución de prestigio nacional verdadera. Esto cambiaría la vida de Peirce larga asociación con la Universidad de Harvard, como su influencia cada vez mayor. Benjamin era un alumno de la Escuela de Gramática Salem privado y no se hizo amigo de Henry Ingersoll Bowditch que fue uno de los ocho hijos de Nathaniel Bowditch y su esposa Mary Ingersoll.
Peirce entró en la Universidad de Harvard en 1825 y se graduó cuatro años después. Durante estos años ha asistido el padre de su amigo Ingersoll Bowditch. Bowditch 's traducción de los cuatro primeros volúmenes de Laplace' s Traite de Mécanique celeste se había terminado en 1818 pero aún no había publicado durante los años que Peirce era estudiante. Casi con toda certeza el costo de la publicación causado el retraso, pero Bowditch no había puesto el trabajo por un lado, después de 1818, aún sigue mejorando lo largo de los años siguientes. Mientras era estudiante, Peirce se involucró en Bowditch 's proyecto y trabajaron a través del texto haciendo lectura de pruebas y sugerir mejoras.
Peirce enseñó en la Ronda George Bancroft Hill School en Northampton, Massachusetts, desde 1829 hasta 1831, y luego fue designado como profesor en la Universidad de Harvard en 1831, dos años después de graduarse. Fue galardonado con un Master de Harvard en 1833 y en el mismo año se casó con Sarah Hunt Mills, la hija del senador Elías Hunt Mills. Benjamin Peirce y Sarah tenía cuatro hijos y una hija, entre ellos Charles Peirce (que también tiene una biografía en este archivo) y James Mills Peirce, que enseñó en el Departamento de Matemáticas en Harvard, y luego desde 1890 hasta 1895 se desempeñó como Decano de la Graduate Escuela de Harvard y, después de que, como Decano de la Facultad de Artes y Ciencias. Sus otros dos hijos también disfrutó de una carrera exitosa, Benjamin Mills Peirce como ingeniero de minas y Herbert Henry Davis Peirce como un diplomático.
Fue en Harvard que Peirce se pasó toda su carrera desde 1831. Nombrado profesor de matemáticas y filosofía natural que en 1833 ocupó este cargo durante nueve años hasta que la cátedra de Matemáticas y Astronomía quedó vacante cuando fue trasladado a esa silla. Su primera silla, no estaba dotado, pero el Presidente fue nombrado en 1842 fue la cátedra Perkins dotado y se fue a celebrar este hasta su muerte.
En la primera parte de su carrera Peirce publicó una serie de libros de texto. Por ejemplo, un tratado elemental Trigonometría en el avión (1835), Primera Parte de un tratado elemental de trigonometría esférica (1936), un tratado sobre la buena Primaria (1936), un tratado sobre álgebra elemental: Para los que se añaden ecuaciones exponenciales y logaritmos (1937 ), un tratado elemental sobre planos y sólidos Geometría (1937), un tratado de Primaria en el avión y Trigonometría Esférica (1940), y un tratado de Primaria en las curvas, funciones y Fuerzas Vol. 1 (1841), Vol. 2 (1846). Estos libros fueron originales y matemáticamente elegante, pero eran demasiado exigentes para los estudiantes americanos de la época. Los estudiantes encontraron demasiado concisa y todos pero los mejores estudiantes también encontró su estilo de conferencias muy difícil; --
Ha dado conferencias sin parar para preguntas y llenó la pizarra con una masa de garabatos. Los mejores estudiantes, sin embargo, fueron capaces de apreciar sus peculiaridades y fueron inspirados por su entusiasmo por las matemáticas.
En Archibald cita la opinión de Lawrence Lowell, uno de los mejores estudiantes que Peirce enseñó:
Tan pronto como terminó el problema o llena la pizarra se frotaba todo y empezar de nuevo. Estaba impaciente de detalle y, a veces el resultado no saldría bien, pero en lugar de ir por encima de su trabajo para encontrar el error, le raspaba, diciendo que había cometido un error en un signo en algún lugar, y que debemos encontrar cuando nos fuimos encima de nuestras notas. Descrito de esta manera, puede parecer extraño que un método de enseñanza debe ser inspirador y, sin embargo para nosotros era así el más alto grado. Fuimos arrastrados por el torrente de su pensamiento, por la facilidad y el alcance de su movimiento intelectual.
Si el estudiante promedio no puede hacer frente a las matemáticas que Peirce fue su presentación para, a continuación, decidió que era mejor sólo vio la más talentosos y dedicados estudiantes continúan con las matemáticas más allá de su primer año. Propuso tres temas diferentes de los que los estudiantes podrían hacer una elección. Una opción era un curso de un año de práctica, el segundo fue un curso de un año teórico diseñado principalmente para maestros de escuela, y la tercera opción era un curso de tres años que los matemáticos de tren del futuro. Después de la Escuela Científica Lawrence fue fundada en Harvard en 1847, Peirce fue capaz de enseñar las matemáticas a nivel de postgrado por primera vez en los Estados Unidos. El curso que organizó fue impresionante, incluyendo el estudio de las obras de Lacroix, Cauchy, Monge, Biot, Hamilton, Laplace, Poisson, Gauss, Le Verrier, Bessel, Adams, Airy, MacCullagh y Franz Neumann. Fue un verdadero curso de la ambición, pero fue un poco por delante de su tiempo y le enseñó a sólo dos alumnos por año.
Peirce emprendió una investigación sobre una amplia gama de temas de matemáticas de la mecánica celeste y geodesia en la parte práctica asociativa al álgebra lineal y teoría de números en el lado puro. En un documento de principios de teoría de números, demostró que no hay ningún número perfecto impar con menos de cuatro factores primos distintos. También revisó y escribió un comentario sobre Bowditch 's traducción de los cuatro primeros volúmenes de Laplace' s Traité de Mécanique celeste que él mismo había tenido la prueba de leer como un estudiante universitario. Sólo tres de estos volúmenes aparecieron en Bowditch 's de por vida, y el propio Peirce completado la edición del cuarto volumen y vio a través de la publicación.
Peirce ayudó a determinar la órbita de Neptuno (descubierto en 1846) y se calculan las perturbaciones producidas por Neptuno en la órbita de Urano y en los otros planetas. De hecho, tenían opiniones controvertidas sobre este tema pues alegó que las predicciones de la posición del planeta Urano perturbadora como realizados por Le Verrier y Adams no coincide con el planeta Neptuno, que descubrió Galle. También afirmó que Neptuno no seguía la órbita prevista por Le Verrier y Adams.
En 1852, Peirce introdujo en los métodos de la teoría de errores aplicados a las observaciones que permitan observaciones defectuoso a ser descartados. Hubo una consecuencia interesante de esto, a saber, que fue llamado como testigo experto en un caso judicial en el 1856 (ver). El caso se refería a la falsificación de la firma de Sylvia Ann Howland, en una voluntad impugnada. Peirce examinó los treinta líneas a la baja en la firma y se mide el ángulo de cada uno. Luego dijo que la comparación de estos ángulos con los de otra de las firmas Sylvia Ann Howland era tan grande que la firma presuntamente falsificada se debe en realidad una falsificación y que han sido localizados. Para respaldar sus alegaciones de que hizo un análisis estadístico de los ángulos de los descendentes de 42 firmas auténticas Sylvia Ann Howland. Existen debilidades en los argumentos estadísticos de Peirce que se señalan en, en especial sobre la independencia de las probabilidades de que él cuenta. Tal vez fue una suerte que el caso se decidió sobre la base de una formalidad legal y las pruebas de Peirce no era crucial en la determinación del resultado del caso. Una de las cosas buenas es que los autores dan todas las firmas que Peirce trabajado, para que todos podamos jugar a los peritos que nosotros mismos!
En 1870 Peirce publicó, a sus expensas, Álgebra Lineal asociativa de una clasificación de todas las álgebras compleja dimensión asociativa de menos de siete. Usó la, ahora familiar, herramientas de elementos idempotente y nilpotente (términos inventados por Peirce) para establecer las bases de una teoría general de álgebra lineal asociativa y presentó las tablas de multiplicar por más de 150 nuevas álgebras en el libro. Había estado muy influido por Hamilton 's trabajar en el cuaterniones para desarrollar esta línea en particular de pensamiento algebraico. Pycior discute este trabajo en donde dice:
Benjamin Peirce merece un reconocimiento, no sólo como uno de los fundadores de las matemáticas de América, sino también como uno de los fundadores del álgebra abstracta moderna.
Peirce leer el texto antes de la Academia Nacional de Ciencias en Washington en 1870 antes de circular 100 copias litografiadas:
Peirce había presentado algunos de sus resultados desde 1867 a la Academia Nacional de Ciencias, de la que había sido nombrado miembro fundador de cuatro años antes, pero que no podían permitirse el lujo de imprimir. Así, en una iniciativa tomada por Costa equipo de prospección, una mujer sin formación matemática, sino que posee una excelente mano se encontró que ambos podían leer su script horrible y escribir el texto completo de 12 páginas a la vez sobre las piedras litografía.
Su hijo Charles Peirce después editó la obra para su publicación en el American Journal of Mathematics en 1881.
Pero hay otra cara a la carrera de Peirce, que todavía tenemos que mencionar. Estuvo involucrado en una forma importante en el United States Coast Survey, como director de las determinaciones de longitud en 1852 luego que se hizo director de la United States Coast Survey en 1867 sobre la muerte del entonces director Alexander Dallas Bache. Continuó como director hasta 1874 y así como la supervisión de la producción de un mapa de los Estados Unidos, organizó expediciones por la Encuesta a Sicilia, Nagasaki, las Islas Chatham, y Alaska para observar eventos astronómicos. Él dijo en su discurso como el final de su presidencia de la Asociación Americana para el Año 1853:
En astronomía ... es preciso reconocer que Saturno y Júpiter, Marte y Venus, están todavía sujetas a las irregularidades inexplicables del movimiento, que la teoría de los asteroides no ha avanzado más allá de la primera etapa de la aritmética, que los anillos de Saturno están relacionados con su principal por un [misterioso] ... la fuerza y las leyes bajo las cuales las mareas obedecer las atracciones del sol y la luna son muy poco desarrolladas. El notable las investigaciones sobre este tema realizados en el Coast Survey, han establecido que aquí todavía queda un mundo por conquistar ...
En Peirce muestra que él cree firmemente en las matemáticas:
... es el gran maestro de clave, que abre todas las puertas del conocimiento, y sin que ningún descubrimiento - ningún descubrimiento que merece el nombre, que es la ley y no un hecho aislado - ha sido o puede ser hecho.
Sin embargo, advierte contra la matemática pura por sí misma:
Fascinado por su simetría, el geómetra puede, a veces, han sido demasiado exclusivamente ocupado con su ciencia, olvidándose de sus aplicaciones; puede haber exaltado a su ídolo, y lo adoraron; puede haber degradado en su juguete, e infantilmente se divertía con las formas singulares que asumiría, cuando debería haber estado trabajando duro con él, que utilizan para el beneficio de la humanidad ...
Teniendo en cuenta esta declaración es un poco extraño que Peirce ha sido llamado el "Padre de la matemática pura" en Estados Unidos (véase, por ejemplo).
Benjamin Peirce recibido numerosas distinciones por sus destacadas contribuciones a la matemática estadounidense. Trabajó para el establecimiento de la Asociación Americana para el Avance de la Ciencia (fundada en 1847) y la Academia Nacional de Ciencias (Estados Unidos) (fundada 1863). Peirce fue uno de un comité de cinco establecido por la Academia Americana de Artes y Ciencias en 1847 para organizar la Smithsonian Institution. También fue nombrado a un consejo científico de tres que organizó el Observatorio de Dudley en Albany, Nueva York, desde 1955 hasta 1858. Peirce fue elegido miembro de la American Philosophical Society (1842), la Royal Astronomical Society (1850), y la Royal Society (1852).
Hagamos por fin tenga en cuenta que Peirce fue un devoto cristiano y vio:
... las matemáticas como el estudio de la obra de Dios por las criaturas de Dios.
Peirce se expande sobre esto a fondo en. Le damos una cita breve:
Hay suficientes pruebas proporcionadas por todas las ciencias, pero ninguno más que la geometría, que el mundo a la que se nos ha asignado es particularmente adaptado a nuestras mentes, y admirablemente equipado para promover nuestro progreso intelectual. No puede haber ninguna duda razonable de que era parte del plan del Creador. ¿Cómo podría fácilmente toda la Orden se han incorporado! ¿Cómo podría fácilmente se nos ha asignado a algún sistema complicado que nuestra débil y limitado las competencias no han descifrado!
tomado de:http://www.learn-math.info/mathematicians/spanish/historyDetail.htm?id=Peirce_Benjamin
http://ztfnews.wordpress.com/2014/04/04/la-matematica-es-la-ciencia-que-senala-las-conclusiones-necesarias/

 Como ya hemos estudiado, tenemos que calcular una matriz A-1que multiplicada por la matriz A obtengamos el resultado:
Como ya hemos estudiado, tenemos que calcular una matriz A-1que multiplicada por la matriz A obtengamos el resultado: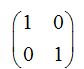
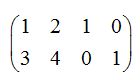
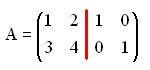
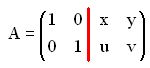
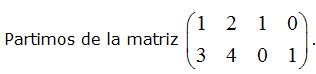
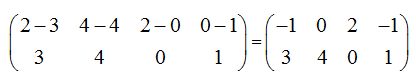

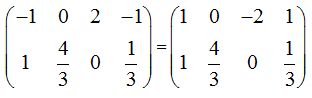
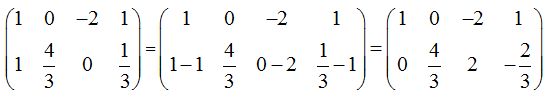
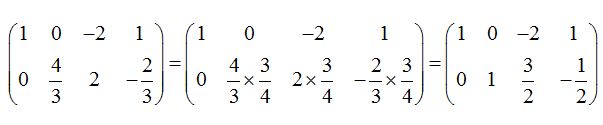
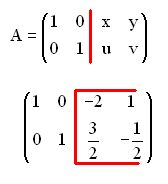
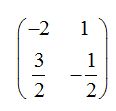
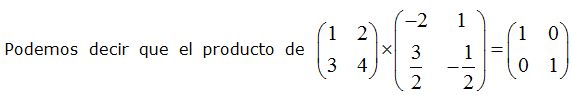 Comprobamos:
Comprobamos: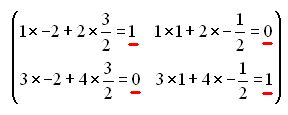
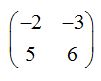
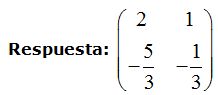

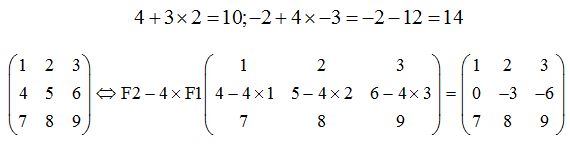
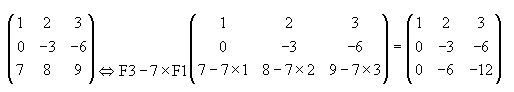
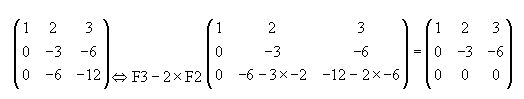
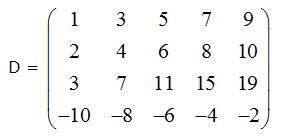
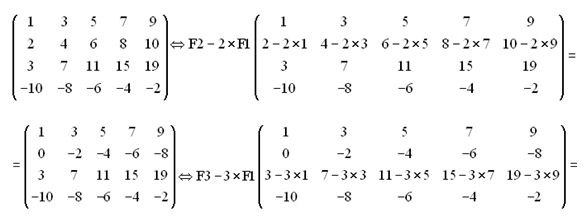
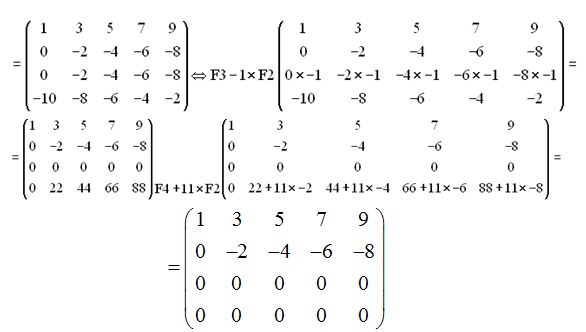
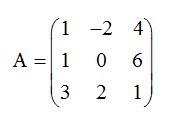 Respuesta: r(A) vale 3
Respuesta: r(A) vale 3