Recordarás que al estudiar por vez primera la matriz inversa dijimos que más adelante volveríamos a estudiarla introduciendo una pequeña variante debido a Carlos Federico Gauss un prodigio de inteligencia desde su más tierna infancia que vivió entre los años 1775 al 1855 en Alemania.
Como ya hemos estudiado, tenemos que calcular una matriz A-1que multiplicada por la matriz A obtengamos el resultado: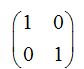
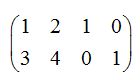
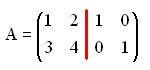
A la derecha de la raya roja la matriz identidad, a la izquierda la matriz propuesta.
Hemos de conseguir que a la izquierda de la vertical de color rojo aparezca la matriz identidad y a la derecha los elementos de la matriz inversa:
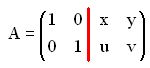
Cuando a la matriz propuesta la hayamos transformado en matriz identidad, los elementos que ocuparán su lugar original será el valor de la matriz inversa (x, y, u, v).
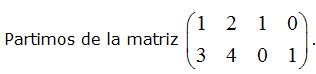
El 2 que ocupa el lugar (1 2) debe darnos un 0 y para ello realizo las siguientes operaciones: F1 = 2F1 – F2:
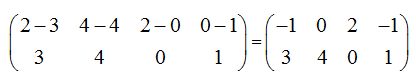
El 3 que ocupa el lugar (1 2) nos interesa vamos a convertirlo en 1, para ello tendremos que dividir a todos los elementos de la fila entre 3:
Multiplicamos por –
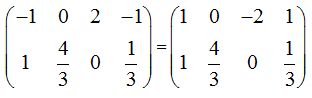
El valor del elemento (2 1) debe tener el valor 0 y para ello realizo la operación: F2 = F2 – F1:
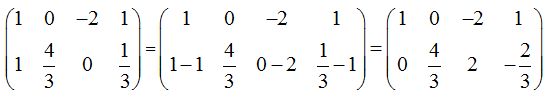
Necesitamos que el valor del lugar (2 2) sea igual a 1 y para ello multiplico a cada uno de los elementos de la fila por 3/4:
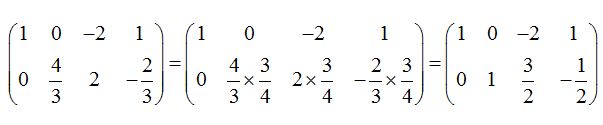
Ya hemos concluido, la matriz inversa es lo que se halla a la derecha de la matriz identidad:
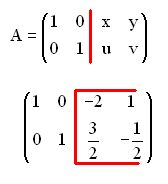
es decir :
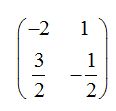
Estos valores corresponden a x, y, u, v.
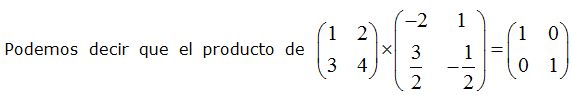Comprobamos: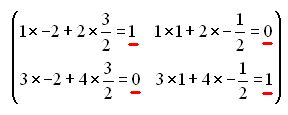
No es complicado calcular la matriz inversa, lo malo es el tiempo que hay que utilizar en resolver y lo fácil que es equivocarse.
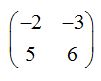
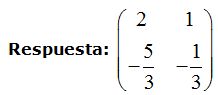
Ejercicio #32
Calcula la matriz inversa de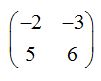
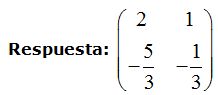
tomado de: http://www.aulafacil.com/matematicas-matrices-determinantes/curso/Lecc-15.htm
No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.