Derivadas y aplicaciones de las derivadas
En esta unidad continuamos el bloque de contenidos de Análisis Matemático o funciones, y lo hacemos subidos a hombros de un auténtico gigante como es la DERIVADA. Sí, la derivada, un aunténtico gigante que como irás viendo, es una potentísima herramienta matemática que aplicada a funciones nos permitirá resolver y descubrir un montón de cuestiones.
La derivada es el ritmo de cambio de cualquier función en un determinado instante, pero que también puede representar el ritmo o velocidad de cambio de cualquier cosa, la densidad o aumento de la población de delfines en relación con el aumento o disminución de la temperatura del agua, el ritmo de cambio de volumen de un globo respecto al área de su superficie o el ritmo de cambio del precio de una pizza con respecto a su tamaño.
Veremos cómo la derivada es para la rama de la Física que estudia las leyes del movimiento, lo que las ruedas son para un viaje, un medio sencillo pero muy eficaz.
Cuando empezamos este bloque de contenidos, lo primero que hicimos fue repasar las propiedades gráficas que tenía una función, ¿por qué?, pues porque es importante conocerlas ya que con un simple vistazo podemos saber toda la información que ésta aporta.
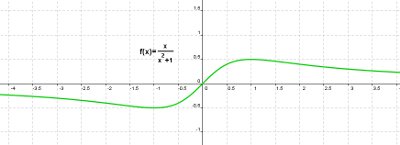El segundo paso, fue repasar las que llamábamos funciones elementales, y recordar cómo se representaban pues a partir de la gráfica lo sabíamos todo, pero claro, hay muchas más funciones, y sería interesante saber también cómo es la forma de todas ellas. La expresión algebraica o analítica nos da la exactitud, pero la expresión gráfica es la que nos aporta visualmente gran información. Por ejemplo, si tenemos la función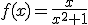
en principio nos quedamos igual, sin embargo, si vemos su gráfica, que es la que aparece a la izquierda, sabemos que para valores grandes,positivos o negativos, se acerca a cero, que primero decrece, después crece y después vuelve a bajar, que si x es menor que cero la función es negativa y a partir de cero positiva, que el valor máximo se alcanza si x vale 1 y es 0,5...
Pero, ¿podré yo dibujar esa función? Pues bien, este es el objetivo principal que nos hemos planteado para este bloque de contenidos, que si tienes cualquier función, sepas representarla gráficamente y por tanto sepas hacer un estudio de todas sus propiedades. Así que, a partir de ahora, podrás sacarle a cualquier función toda la información que posea. ¡Ya les gustaría a los detectives tener algo así!
En la última parte del tema, aprenderás también una técnica basada en las derivadas de funciones importantísima e interesantísima, pues busca obtener siempre la mejor respuesta ante una determinada situación. Vas a ver cómo la derivada se puede aplicar al diseño de una parcela, a la recogida de frutos o a la fabricación de envases.
1. Tasa de variación media e instantánea. Definición de derivada.
Dada una función f(x), llamábamos tasa de variación al número que representa el aumento o disminución que experimenta la función al aumentar la variable independiente de un valor "a" a otro "b".
La tasa de variación de f(x) entre a y b (siendo a
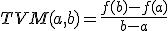
La tasa de variación de f(x) entre a y b (siendo a
TV[a,b]= f(b)-f(a).
La tasa de variación media de una función f(x) entre a y b (siendo a), la definíamos que la variación media que se producía en el intervalo:
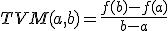
Si en lugar de "b", al segundo punto lo llamamos "a+h", la fórmula anterior quedaría así:
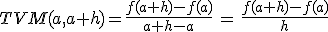
Si hacemos h muy pequeño, obtenemos una información precisa de lo que ocurre en el punto de abscisa a. Y hacer h muy pequeño, es hacerlo tender a cero. Pues bien cuando hacemos h tender a cero en la tasa de variación media, llegamos al concepto de tasa de variación instantánea. Es decir, la tasa de variación instantánea en un punto, es el límite cuando h tienede a cero de la tasa de variación media en el intervalo [a, a+h]
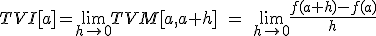
Y esto precisamente nos lleva al concepto de derivada en un punto; la variación instantánea en un punto. Así, la derivada de una función f(x) en el punto de abscisa x0, se define como el límite:
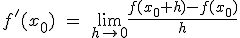
2. Derivada de funciones
Cuando has visto el último vídeo seguro que has dicho -Claro así es más fácil. Primero derivo y después sustituyo-.
La derivada de las funciones, salen de hacer los límites de la definición, pero en general; sin poner ningún punto en concreto, o lo que es lo mismo, dejando la variable independiente "x".
Es decir,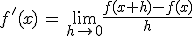 
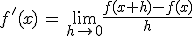
Regla de la cadena
Para derivar una función compuesta, utilizamos la llamada regla de cadena, que consiste en ir derivando cada función que nos vamos encontrando respetando su argumento y multiplicando por la derivada de ese argumento:
f(g(x))' = f '(g(x))·g'(x)
