Se dice que un día Aquiles, el más grande de los guerreros, héroe de Troya y verdugo de Héctor en combate singular, fue retado a una carrera no por un campeón que anhelara arrebatarle su gloria, sino por una simple tortuga. Aquiles, sorprendido, rechazó el duelo por considerarlo poco digno de su condición de hijo de Dioses, pero la tortuga se mostró tenaz y propuso que, para anular toda superioridad que pudiera tener, este no tomaría la salida hasta que ella hubiese ganado nada más y nada menos que un
estadio de ventaja.
Finalmente Aquiles dio su aún invicto brazo a torcer y accedió a aceptar tan extravagante reto, pues consideró que la ventaja que daba a la tortuga era tal que permitiría afianzar aún más su reconocimiento como el más veloz de los hombres. La carrera comenzó, y Aquiles esperó a que la tortuga recorriera el primer estadio con la paciencia de la que sólo es capaz el guerrero que ha velado mil batallas. Cuando lo hizo, se lanzó como un rayo hacia la meta deslizándose sobre el suelo tan rápido que habría dejado atrás al más veloz de los corceles, pero a la vez tan grácilmente que habría ganado con facilidad el favor de la damisela de corazón más frío.

Llegó Aquiles al primer estadio y vio que la tortuga había recorrido apenas sesenta
pies. Pensó que ya tenía la carrera ganada, pues corría diez veces más rápido que su rival, pero cuál fue su sorpresa al ver que, al avanzar esos sesenta pies, la tortuga se encontraba todavía a seis pies de distancia. Recorrió esos seis pies decidido a dar alcance a la tortuga, pero para cuando lo logró ésta se hallaba a tres quintas partes de un pie de donde él se encontraba. Y aunque Aquiles alcanzó pronto esas tres quintas partes, para cuando llegó la tortuga ya había conseguido avanzar tres partes entre cincuenta más. De esta manera Aquiles,
el de los pies ligeros, nunca fue capaz de dar alcance a la tortuga, pues cada vez que llegaba al lugar donde ella había estado un instante antes ésta ya se había desplazado un poco más allá.
Esta historia (de la que me he permitido redactar una versión libre) es una de las conocidas
paradojas de Zenón, concretamente la paradoja de
Aquiles y la tortuga. Se trata de un
sofisma, un razonamiento lógico que aparenta ser correcto pero no lo es, pues evidentemente Aquiles le pegaría una soberana paliza a la tortuga en una carrera real. Existen muchas formas de rebatir a Zenón en su paradoja (como pueden comprobar
aquí), pero más que hablarles de lo acertado o no del relato, me gustaría describir un concepto matemático de gran importancia que se esconde en él: el de
lo infinitamente pequeño.
Probablemente sin ser consciente de ello Zenón aportó uno de los mejores ejemplos que existen para

entender que el infinito no consiste simplemente en comenzar a contar y no parar jamás. El concepto clásico de infinito, el que relacionamos intuitivamente con las cosas infinitamente grandes, es el referido al cardinal de los números naturales, es decir, a la cantidad de números naturales que existen. Sin embargo lo que se describe en la paradoja es una idea muy diferente.
Aquiles, aunque va 10 veces más rápido que la tortuga, recorre primero 1 estadio (600 pies), a los que suma 60 pies, después 6 pies más, luego otros 6/10=3/5, y así va añadiendo sucesivamente 3/50, 3/500, 3/5000 pies… Como se puede seguir indefinidamente dividiendo por diez cada distancia recorrida, en su camino para alcanzar a la tortuga Aquiles se ve obligado a recorrer una cantidad infinita de espacios que llegan a ser infinitamente pequeños, en el sentido de que, por muy reducidos que sean, el espacio siguiente siempre será más diminuto que el anterior.
Más aún, si aplicamos el mismo razonamiento a su rival, la tortuga irá poniendo también de por medio infinitos espacios infinitamente pequeños, manteniéndose siempre alejada de su perseguidor aunque sólo sea por un poco. Como además no parece posible recorrer infinitos espacios en un tiempo finito, Zenón concluye que Aquiles nunca alcanzará a la tortuga.
Estos espacios representan un concepto de infinito, diferente al de los números naturales y que podemos relacionar con lo infinitamente pequeño, que surge del hecho de que entre dos números cualesquiera siempre se pueden encontrar infinitos números más, por ejemplo: entre el 666 (600+60+6) y el 667 encontramos el 666.6 (666+3/5), el 666.66 (666.6+3/50), 666.666 (666.66+3/500) etcétera. Basándose en esta propiedad Zenón concluyó en su paradoja que, debido a que el espacio se puede dividir en trozos infinitamente pequeños, el movimiento no era posible, y por tanto debía ser mera ilusión.
Pero la realidad no es así, y lo sabemos. ¿Quién se equivoca entonces? ¿Las matemáticas o Zenón? Aunque hoy en día nos pueda parecer absurdo Zenón tenía razones sólidas para pensar que su conclusión era la acertada, pues en su forma de pensar la razón era una herramienta más potente y mucho más fiable que los sentidos, que nos pueden engañar fácilmente. Así, si utilizando la lógica se llegaba a la conlusión de que el movimiento no era posible, entonces es que no lo era por mucho que nuestros ojos vieran a Aquiles adelantar a la tortuga.
Pero las matemáticas por aquella época andaban aún en pañales y con las herramientas que se manejaban entonces no era fácil dar con una explicación que convenciera al bueno de Zenón (por no decir que era imposible). Sin embargo, alrederor de dos mil años después se encontró una forma de sumar cantidades infinitamente pequeñas como las que aquí aparecen, y además cuando se logró los matemáticos se dieron cuenta que algunas de estas sumas dan lugar a valores finitos. Y por suerte para Aquiles, las sumas infinitas que la tortuga pretendía utilizar para ganar la carrera son de estas últimas (pueden ver en esta figura cuál es el valor de la suma en este caso).

Aquiles alcanza a la tortuga a los 2000/3 pies de su salida
Por lo tanto las matemáticas acabaron por resolver la paradoja* demostrando que, aunque Aquiles necesita recorrer infinitos tramos infinitamente pequeños para alcanzar a la tortuga, éstos sumados forman una distancia finita que se puede recorrer en un tiempo determinado. Y así al final Aquiles alcanza a la pobre tortuga, que derrotada no puede hacer más que rendirse ante la evidencia.
- Bueno, lo importante es participar – dijo la tortuga con resignación cuando el hijo de Tetis pasó a su lado corriendo como si persiguiera al mismísimo Ares.



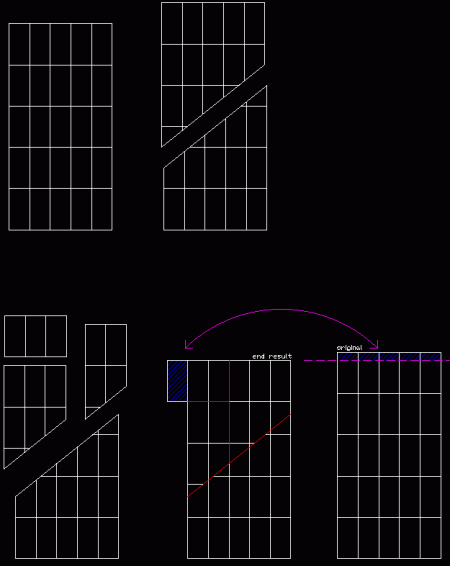

 entender que el infinito no consiste simplemente en comenzar a contar y no parar jamás. El concepto clásico de infinito, el que relacionamos intuitivamente con las cosas infinitamente grandes, es el referido al cardinal de los números naturales, es decir, a la cantidad de números naturales que existen. Sin embargo lo que se describe en la paradoja es una idea muy diferente.
entender que el infinito no consiste simplemente en comenzar a contar y no parar jamás. El concepto clásico de infinito, el que relacionamos intuitivamente con las cosas infinitamente grandes, es el referido al cardinal de los números naturales, es decir, a la cantidad de números naturales que existen. Sin embargo lo que se describe en la paradoja es una idea muy diferente.