Interpolación lineal

7 de mayo de 2013 Publicado por Laura

La interpolación lineal es un procedimiento muy utilizado para estimar los valores que toma una función en un intervalo del cual conocemos sus valores en los extremos (x1, f(x1)) y (x2,f(x2)). Para estimar este valor utilizamos la aproximación a la función f(x) por medio de una recta r(x) (de ahí el nombre de interpolación lineal, ya que también existe la interpolación cuadrática).
La expresión de la interpolación lineal se obtiene del polinomio interpolador de Newton de grado uno:

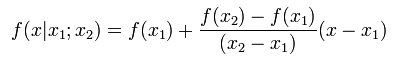
RECTA DE INTERPOLACIÓN LINEAL
Veamos los pasos que tenemos que seguir para hallar la recta de regresión:
1º. Dados los puntos de la función (x1, y1) y (x2, y2), queremos estimar el valor de la función en un punto x en el intervalo x1
2º. Para hallar la recta de interpolación nos fijaremos en la siguiente imagen.


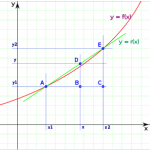
Para ello utilizamos la semejanza de los triángulos ABD y CAE, obteniendo la siguiente proporcionalidad de segmentos: AB/AC=BD/CE.
3º. Despejando el segmento BD (ya que el punto D es el que desconocemos) obtenemos:
BD=(AB/AC)∙CE. Traduciendo al lenguaje algebraico obtenemos que:

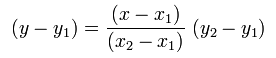
Y despejando y, obtenemos:

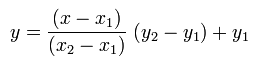
La misma expresión que se obtiene al utilizar el polinomio interpolador de Newton que ya habíamos comentado. Recordad que y1=f(x1) y análogamente y2=f(x2).

Ejemplo:  En una determinada empresa de conservas se hace un estudio de los ingresos que se obtienen a partir de los gastos. Estos datos se recogen en la siguiente tabla (en miles de euros).

A partir de los datos recogidos en la tabla, calcular:
a) Los ingresos que se pueden esperar si hemos realizado un gasto de 4000 euros.
b) Los ingresos obtenidos si en esta ocasión el gasto es de 6000 euros.
En primer lugar podemos comenzar representado los datos facilitados por la tabla en el eje de coordenadas ( no es obligatorio pero nos facilita la visión del ejercicio).


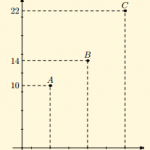
Como no conocemos la función mediante la que se han obtenido los datos, vamos a utilizar la interpolación lineal.
a) Cuando x=4, vamos a utilizar los datos que nos proporciona la tabla x1=3 y x2=5, cuyos valores respectivos son f(x1)=10 y f(x2)=14.
Utilizando la fórmula de interpolación mencionada, sustituimos los valores que mencionados obteniendo:

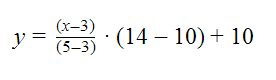
Sustituyendo el valor de x que nos piden: x=4, (recordar que los datos vienen dados en miles de euros) obtenemos el valor de ingresos esperado:

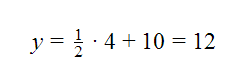
Por tanto, si hay un gasto de 4000 euros se obtendrán unos ingresos de 12000€.

b) De forma análoga al apartado anterior, en este caso tenemos que repetir la interpolación, ya que ahora el valor que nos piden es x=6 (no os olvidéis que los datos están dados en miles de euros), y esta valor está entre 5

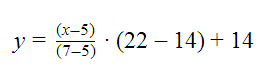
Donde al sustituir por 4 obtenemos:

Por tanto, si el gasto es de 6000 euros, los ingresos obtenidos serán de 18000 euros.

Lee todo en: Interpolación lineal | La Guía de Matemática http://matematica.laguia2000.com/general/interpolacion-lineal#ixzz377UUMabD

Evolución de los números

19 de febrero de 2014 Publicado por Laura

A lo largo de la historia el ser humano siempre ha tenido la necesidad de contar, de expresar operaciones mercantiles y de resolver otros problemas que han ido surgiendo en el desarrollo de las matemáticas.
Analizaremos la evolución de los diversos conjuntos, de tal forma que cada uno de ellos esté contenido en el siguiente. No obstante, la evolución de estos números puede ser que coincida en el tiempo.

Los números naturales:

Desde el comienzo de la humanidad las diferentes culturas han empleado diversas formas de contar, ya sea utilizando piedras, muescas en palos e incluso los dedos de las manos y los pies. Sin embargo, no fue hasta el siglo IX d.C, gracias a Al-Khwarizmi cuando se adopta el sistema de numeración hindú. No obstante, en Europa tendremos que esperar hasta el siglo XIII para que los números naturales lleguen. Estableciéndose de manera formal en el siglo XIX gracias a Peano, a quien debemos la definición axiomática de los números naturales.

Los números enteros:

La solución de ecuaciones del tipo x+a=b, donde a>b, no tienen cabida en el cuerpo de los números naturales. Necesitamos ampliar el conjunto y definir de esta forma los números negativos. Estos números surgieron por la necesidad de operar con cantidades negativas, sobre todo en las operaciones comerciales. Los primeros en introducir los números negativos fueron los hindúes, en concreto, Brahmagupta. A Europa llegan a finales del siglo s.XV gracias al matemático francés Nicolas Chuquet. Si embargo, no fue hasta finales del siglo XIX cuando Weierstrass perfila el modelo de los números enteros, definiéndolos como clases de equivalencias de paras de números naturales.

Los números racionales:

A la hora de resolver la ecuación ax=b, tal que b no es múltiplo de a (es decir, a no es divisor de b), no existe solución en los números enteros. La necesidad de fraccionar la unidad nos lleva a la definición de las fracciones. Aunque se trabaja con ellas desde la antigüedad, pero con notaciones complicadas. Los babilonios comenzaron a utilizar la notación decimal, dividiendo la unidad en potencias sucesivas de 60. Pero fueron los árabes quien establecieron la barra horizontal para separar el numerador y el denominador.

Los números reales:

Aparece un nuevo obstáculo que hace que el cuerpo de los números racionales se quede pequeño, como el de hallar lo que mide la diagonal de un cuadrado de lado 1, o el resultado de la ecuación x al cuadrado igual a 2. Este descubrimiento se produce gracias a la escuela pitagórica, y recibieron el nombre de inconmensurables. No obstante, no fue hasta la llegada del Renacimiento, cuando los matemáticos europeos aprovecharon el sistema decimal, para definir los números irracionales como aquellos números que tienen infinitas cifras decimales.

Los números complejos:

Por último, como obstáculo final nos encontramos con un nuevo problema, ¿qué ocurre cuando al resolver una ecuación de segundo grado o superior obtenemos una raíz cuadrada negativa? Hasta entonces, esta ecuación no tiene solución (de hecho no tiene solución real). Aunque se comenzó a trabajar con estos números como si se trataran de números normales, ya que cumplían una serie de condiciones. El carácter esotérico de estos números se fue eliminando, sobre todo con la obra de Cardano en 1545 “Arg Magna”. Sin embargo, fue Euler el que estableció la notación que ahora conocemos, para denotar la raíz de menos uno como i.

Lee todo en: Evolución de los números | La Guía de Matemática http://matematica.laguia2000.com/general/evolucion-de-los-numeros#ixzz377RJlpOU