miércoles, 23 de julio de 2014
EL POLINOMIO VILLARREAL
El 21 de octubre de 1879 Federico Villarreal presenta su tesis para optar el grado de Bachiller en Matemáticas, la cual estaba conformado de 4 temas:
- Elevación de Polinomios
- Transformación de Imaginarias
- Volumen de Cuerpos Regulares
- Integración por Partes
En el primer tema insertó un método para poder elevar un polinomio a un exponente cualquiera (real o complejo), este método es recursivo y de fácil aplicación. Describirémos este método de la manera como fue planteada en dicha tesis:
Sea 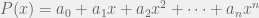 un polinomio, el cual elevaremos al exponente “m” (este puede ser real o complejo) es decir:
un polinomio, el cual elevaremos al exponente “m” (este puede ser real o complejo) es decir:
la expresión resultante la denotamos por:
Notemos que el resultado puede ser otro polinomio de grado “m.n” si el exponente “m” fuera un número entero positivo, en tanto que si fuera real (no entero positivo) o complejo resultaría una serie infinita.
El método de villarreal establece previamente una simbolizaría:
- El primer término del polinomio elevado al exponente de la potencia es el primero del desarrollo, de modo que se puede siempre suponer conocido a lo menos un término de la potencia, así tendremos:
.
- Dividase el
término del polinomio entre el primero y llámese el cociente
, dividase el
término entre el primero y sea el cociente
, el cuarto término entre el primero y sea el cociente
…. es decir dividiendo cada término del polinomio, desde el segundo inclusive entre el primero, se obtendrán tantos cocientes como términos menos uno tiene el polinomio.
- Aumentese uno al exponente de la potencia y llamando su suma i tendremos los índices: i,2i,3i, … es decir multiplicando los números naturales uno, dos, tres,… por el exponente aumentado en uno, se pueden obtener tantos índices como términos menos uno tiene el polinomio.
- Un término cualquiera se forma sumando los productos siguientes: el ultimo termino
multiplicado por el primer cociente C’ y por el índice disminuido en el número de términos sacados y dividido entre el mismo número de términos
, el penúltimo término
multiplicado por el segundo cociente C’’ y por el segundo índice disminuido en el número de términos sacados y dividido entre el mismo número de términos
, el antepenúltimo término
multiplicado por el tercer cociente C’’’ y por el tercer índice disminuido en el número de términos sacados y dividido entre el mismo número de términos
, ……., así tendremos:
EJEMPLO:
Supongamos que deseamos obtener  con una cierta aproximación (por definir), entonces podemos proceder de la siguiente manera:
con una cierta aproximación (por definir), entonces podemos proceder de la siguiente manera:
- Considerar
como el resultado de sacar la raíz cuadrada a la evaluación en un determinado valor de la variable x del polinomio
, es decir:
- La expresión resultante es una serie infinita, cuyos términos podemos calcular uno a uno mediante el método de Villarreal.
Para hacer los cálculos respectivos fijamos la simbología establecida anteriormente:
Ahora recurrimos al método de Villarreal:
Luego obtendremos el siguiente resultado:
Para poder hacer la aproximación adecuada consideramos la condición de convergencia de Newton:
es decir se dá la convergencia si : 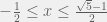
Luego si hacemos 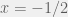 en la expresión resultante:
en la expresión resultante:
Esto significa que la convergencia será mas adecuada si tomásemos más términos en la expresión resultante.
TOMADO DE: http://aprendiendomate.wordpress.com/2009/04/05/el-polinomio-villarreal/
Suscribirse a:
Comentarios (Atom)
Archivo del blog
-
►
2017
(19)
- ► septiembre (1)
-
▼
2014
(441)
- ► septiembre (61)
-
►
2011
(38)
- ► septiembre (4)
-
►
2010
(74)
- ► septiembre (6)
