domingo, 20 de abril de 2014
EL MARAVILLOSO TRIÁNGULO ARITMÉTICO
Dentro de un ciclo de jornadas matemáticas de una Universidad catalana se daba una conferencia titulada "Las Matemáticas durante el Renacimiento", el ponente comenzó su exposición diciendo:
- “U; u, u; u, ... *(en catalán u = uno)
De pronto uno de los asistentes exclama en voz suficientemente alta como para ser oído por la mesa:
- ¡Vaya, nos ha tocado un “tartajas”!
Entonces el ponente, con mucha calma, retomó su conferencia:
- “Bien, como las iba diciendo, u; u u; u dos u; u tres tres u; ... algunos de ustedes ya se habrán dado cuenta que no se trata de un “tartajas” sino de Tartaglia, más concretamente del archiconocido triángulo de Tartaglia, atribuido también a Pascal o, en países asiáticos, a Yang Hui. Sin duda, se trata de una de las joyas de la matemática, datado durante el Renacimiento en Europa, con el que quería comenzar esta exposición ...”
- “U; u, u; u, ... *(en catalán u = uno)
De pronto uno de los asistentes exclama en voz suficientemente alta como para ser oído por la mesa:
- ¡Vaya, nos ha tocado un “tartajas”!
Entonces el ponente, con mucha calma, retomó su conferencia:
- “Bien, como las iba diciendo, u; u u; u dos u; u tres tres u; ... algunos de ustedes ya se habrán dado cuenta que no se trata de un “tartajas” sino de Tartaglia, más concretamente del archiconocido triángulo de Tartaglia, atribuido también a Pascal o, en países asiáticos, a Yang Hui. Sin duda, se trata de una de las joyas de la matemática, datado durante el Renacimiento en Europa, con el que quería comenzar esta exposición ...”
· Niccolo Fontana más conocido como Tartaglia, nació en Brescia en el año 1.499, y murió en Venecia el 13 de diciembre de 1.557. Era hijo de un humilde cartero.
A los doce años, sobrevivió milagrosamente cuando en 1.512 los franceses invadieron su villa provocando una monstruosa matanza, aunque las horribles cicatrices que le quedaron en la cara le obligaron a llevar barba toda su vida adulta, además, al ser afectadas sus cuerdas vocales, hablaba con dificultades y de aquí el sobrenombre de Tartaglia, que quiere decir tartamudo en italiano.
Fue el primer matemático en idear un procedimiento general de resolución de las ecuaciones de tercer grado, manteniendo en secreto sus métodos.
Cardano, otro gran matemático italiano de la época, le engañó prometiéndole que él también los mantendría en secreto, sin embargo, faltó a su palabra de honor y los publicó en su obra Ars Magna.
Tartaglia publicó en 1.537 su primer libro sobre teoría balística.
· Blaise Pascal nació en Clermont el día 19 de agosto de 1.623.
Era hijo de un insigne magistrado y estudioso de problemas físicos y matemáticos, recibió de éste su primera formación. En 1.631 se trasladaron a París y frecuentaron el círculo de intelectuales organizado por Mersenne. Pronto destacó por sus investigaciones en geometría y física. A los 15 años publicó "Ensayo sobre las cónicas".
Sobre 1.646 se adhirió al jansenismo, hecho que marcó para él, el comienzo de sus preocupaciones por el estudio del hombre, pero sin abandonar el campo científico. Desarrolló la teoría de las combinaciones, creó las bases del cálculo de probabilidades, y estudió la cicloide.
En física, publicó la obra “Nuevos experimentos entorno al vacío” (1.647) y elaboró el principio que lleva su nombre y que dice: Toda presión ejercida sobre un líquido, se transmite por igual a todos los puntos de su masa y actúa perpendicularmente sobre las paredes del recipiente que lo contiene.
Publicó un tratado sobre el tema que nos ocupa "Triángulo aritmético" (1.654)
En el año 1.654 siente una profunda religiosidad que marcará el resto de su existencia y se une al grupo de los solitarios de Port-Royal, un grupo laico que vivía dedicado a la meditación.
En 1.656 escribe, en contra de la ortodoxia, sus cartas “Provinciales” que fueron condenadas por la Iglesia.
En 1.658 publica su obra póstuma “Pensamientos”.
Debilitada su salud por una larga enfermedad murió el 19 de agosto de 1.662 en París, justo el día de su 39º aniversario, reconciliado con la Iglesia.
Era hijo de un insigne magistrado y estudioso de problemas físicos y matemáticos, recibió de éste su primera formación. En 1.631 se trasladaron a París y frecuentaron el círculo de intelectuales organizado por Mersenne. Pronto destacó por sus investigaciones en geometría y física. A los 15 años publicó "Ensayo sobre las cónicas".
Sobre 1.646 se adhirió al jansenismo, hecho que marcó para él, el comienzo de sus preocupaciones por el estudio del hombre, pero sin abandonar el campo científico. Desarrolló la teoría de las combinaciones, creó las bases del cálculo de probabilidades, y estudió la cicloide.
En física, publicó la obra “Nuevos experimentos entorno al vacío” (1.647) y elaboró el principio que lleva su nombre y que dice: Toda presión ejercida sobre un líquido, se transmite por igual a todos los puntos de su masa y actúa perpendicularmente sobre las paredes del recipiente que lo contiene.
Publicó un tratado sobre el tema que nos ocupa "Triángulo aritmético" (1.654)
En el año 1.654 siente una profunda religiosidad que marcará el resto de su existencia y se une al grupo de los solitarios de Port-Royal, un grupo laico que vivía dedicado a la meditación.
En 1.656 escribe, en contra de la ortodoxia, sus cartas “Provinciales” que fueron condenadas por la Iglesia.
En 1.658 publica su obra póstuma “Pensamientos”.
Debilitada su salud por una larga enfermedad murió el 19 de agosto de 1.662 en París, justo el día de su 39º aniversario, reconciliado con la Iglesia.
· Yang Hui era un oficial menor chino que escribió dos libros, datados en 1.261 y en 1.275.
En ellos, utiliza las fracciones decimales (mucho antes que en Occidente), también aparece documentado el triángulo aritmético.
La referencia más antigua al triángulo aritmético es atribuida a Omar Khayyam, un poeta, matemático y astrónomo persa que, probablemente, precedió a Yang Hui, pero no se tiene certeza de la fecha exacta en que transcurrió su vida.
En ellos, utiliza las fracciones decimales (mucho antes que en Occidente), también aparece documentado el triángulo aritmético.
La referencia más antigua al triángulo aritmético es atribuida a Omar Khayyam, un poeta, matemático y astrónomo persa que, probablemente, precedió a Yang Hui, pero no se tiene certeza de la fecha exacta en que transcurrió su vida.
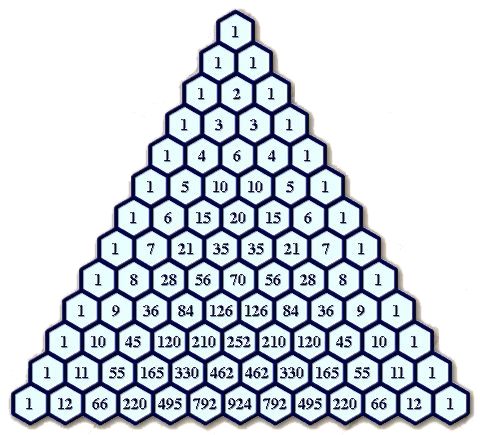
Como muchos de vosotros ya sabréis, este triángulo se genera a partir de colocar el número 1 en su extremo superior y, a partir de aquí, las sucesivas filas se construyen colocando un 1 en cada esquina, el resto de casillas es igual a la suma de los dos números que tiene justo encima –observad la figura- en una infinita serie de unos laterales y de sumatorios de casillas que producen un incesante aumento de los números que lo componen.
Pues bien, esta figura, que podría parecer para los neófitos un simple entretenimiento de cálculo, esconde una diversidad de propiedades y curiosidades tan grande que lo convierten en un pequeño universo matemático en sí mismo y una herramienta de inmensa utilidad en el campo numérico, etc.
Los matemáticos de todas las épocas, desde su descubrimiento, han puesto sus ojos en él y han buscado todo tipo de sorprendentes relaciones, utilidades y recursos.
Y a mí, que también me ha fascinado siempre este triángulo, me ha llevado a hacer una pequeña investigación sobre él, fruto de la cual he hallado algunos aspectos interesantes, aparte de los habitualmente estudiados.
Pues bien, esta figura, que podría parecer para los neófitos un simple entretenimiento de cálculo, esconde una diversidad de propiedades y curiosidades tan grande que lo convierten en un pequeño universo matemático en sí mismo y una herramienta de inmensa utilidad en el campo numérico, etc.
Los matemáticos de todas las épocas, desde su descubrimiento, han puesto sus ojos en él y han buscado todo tipo de sorprendentes relaciones, utilidades y recursos.
Y a mí, que también me ha fascinado siempre este triángulo, me ha llevado a hacer una pequeña investigación sobre él, fruto de la cual he hallado algunos aspectos interesantes, aparte de los habitualmente estudiados.
Comenzaré por partes, e iré enumerando y explicando sus propiedades más características:
- El número 1 de l’extrem superior del triángulo se considera como la fila cero.
- El número 1 de l’extrem superior del triángulo se considera como la fila cero.
- Cada número se genera a partir de la suma de los dos números que tiene encima, como ya dije.
Así, por ejemplo, los dos unos de la fila 1 sumados forman el 2 central de la segunda fila.
La tercera fila se forma a partir del 1 + 2 = 3 y 2 + 1 = 3. La cuarta es 1 + 3 = 4, 3 + 3 = 6, etc.
Así, por ejemplo, los dos unos de la fila 1 sumados forman el 2 central de la segunda fila.
La tercera fila se forma a partir del 1 + 2 = 3 y 2 + 1 = 3. La cuarta es 1 + 3 = 4, 3 + 3 = 6, etc.
- Todas las filas muestran una estructura simétrica, las de orden par tienen un número central único, las de orden impar tienen dos números idénticos en el centro. La suma de cada semifila impar es, obviamente, igual.
- La suma de los números de cada fila es igual a 2 elevado al número de la fila.
La cuarta fila, por ejemplo: 1 + 4 + 6 + 4 + 1 = 16 = 24. La sexta 1 + 6 + 15 + 20 + 15 + 6 + 1 = 64 = 26
La cuarta fila, por ejemplo: 1 + 4 + 6 + 4 + 1 = 16 = 24. La sexta 1 + 6 + 15 + 20 + 15 + 6 + 1 = 64 = 26
- Cada fila expresa las sucesivas potencias del número 11, las cuatro primeras de forma clara, y a partir de la quinta fila, si una casilla está formada por más de una cifra, efectuamos una sencilla suma llevándonos alguna cifra. Ejemplos:
- Si nos situamos en las filas correspondientes a los números primeros observaremos que se forman triángulos invertidos con sus múltiplos siguiendo un patrón infinito y maravilloso que he intentado reflejar en esta ilustración.
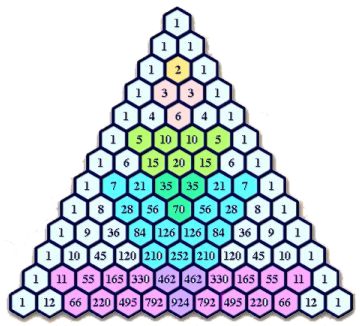
El número 11, aunque no está completo en el gráfico, os garantizo que también lo forma y así los sucesivos números primeros.
Es muy curioso que este patrón sólo se presente en los números primeros y, en cambio, no suceda con el resto de números, observad como falla con los números pares o con el 9, el 15, etc.
Podríais hallar una razón o demostración para esta propiedad. (Demostración)
- La suma de los números unidos por líneas rojas, y situados a salto de caballo, forman la conocida serie de Fibonacci.
Veámoslo: 1, 1, 1 + 1 = 2, 2 + 1 = 3, 1 + 3 + 1 = 5, 3 + 4 + 1 = 8, 1 + 6 + 5 + 1 = 13, 4 + 10 + 6 + 1 = 21, etc.

El número 11, aunque no está completo en el gráfico, os garantizo que también lo forma y así los sucesivos números primeros.
Es muy curioso que este patrón sólo se presente en los números primeros y, en cambio, no suceda con el resto de números, observad como falla con los números pares o con el 9, el 15, etc.
Podríais hallar una razón o demostración para esta propiedad. (Demostración)
- La suma de los números unidos por líneas rojas, y situados a salto de caballo, forman la conocida serie de Fibonacci.
Veámoslo: 1, 1, 1 + 1 = 2, 2 + 1 = 3, 1 + 3 + 1 = 5, 3 + 4 + 1 = 8, 1 + 6 + 5 + 1 = 13, 4 + 10 + 6 + 1 = 21, etc.
- Cada fila determina los coeficientes que se obtienen desarrollando las sucesivas potencias del binomio:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
- Cada término del triángulo se puede expresar como el resultado del número combinatorio:
(n! se lee "n factorial" y se calcula: n! = n·(n - 1)·(n - 2)·... ·2·1. (por ejemplo, 5! = 5·4·3·2·1 = 120)
En el triángulo aritmético n es, también, el número de la fila y m el número de la columna.
Por eso los números del triángulo reciben también el nombre de números combinatorios.
Por ejemplo, la tercera fila está formada por los números combinatorios: C3,0 = 1 ,C3,1 = 3, C3,2 = 3, C3,3 = 1
En la cuarta fila observamos que: C4,0 = 1 ,C4,1 = 4, C4,2 = 6, C4,3 = 4, C4,4 = 1, etc.
El número combinatorio Cn,m representa el número de grupos diferentes de m elementos que se pueden formar a partir de n objetos, combinaciones de n elementos tomados de m en m.
Por ejemplo, si queremos calcular cuantos grupos de 4 miembros se pueden formar dentro de un conjunto de 10 personas, tenemos que el resultado es C10,4; combinaciones de 10 elementos tomados de 4 en 4.
Esto se puede calcular con el algoritmo anterior o bien buscando en el triángulo aritmético: décima fila, cuarto término, dónde obtenemos el valor 210 que es el resultado exacto.
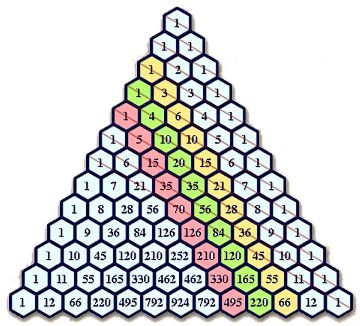
- La segunda diagonal, situada al lado de la diagonal formada por los unos exteriores, contiene la evidente sucesión de números naturales.
- La tercera diagonal, coloreada en amarillo, determina la serie de números triangulares:
La serie de los números triangulares presenta muchas curiosidades o propiedades interesantes, como:
· La suma de dos términos consecutivos an y an-1 de esta serie es igual al cuadrado del número n.
Por ej.: 3 + 1 = 4, 6 + 3 = 9, 10 + 6 = 16, etc.
De hecho, demostrarlo es bastante sencillo:
Por ejemplo: 3 - 1 = 2, 6 - 3 = 3, 10 - 6 = 4, etc. De manera análoga a la anterior demostración tenemos que:
Es decir, también los números cúbicos aparecen en el triángulo aritmético si sabemos buscarlos.
Si tomamos los números de esta tercera diagonal de forma alterna, aparecen los números hexamórficos:
- En la cuarta diagonal, coloreada en verde y formada por la serie: 1, 4, 10, 20, 35, etc., si restamos los números haciendo saltos dobles (con el antepenúltimo) aparece la serie de números cuadrados, o sea:
Además esta diagonal es la serie de los números tetramórficos.
- En la quinta diagonal, coloreada en rojo y compuesta por la serie: 1, 5, 15, 35, 70, 126, etc., si restamos los números efectuando saltos triples aparece la suma del cuadrados mágicos de orden igual al lugar que ocupa el número a la serie, es decir:
15 - 0 = 15 (orden 3, tercer nº de la serie), 35 - 1 = 34(orden 4, cuarto nº.), 70 - 5 = 65 (orden 5, quinto nº)
15 - 0 = 15 (orden 3, tercer nº de la serie), 35 - 1 = 34(orden 4, cuarto nº.), 70 - 5 = 65 (orden 5, quinto nº)
- Se han estudiado además otras propiedades numéricas del triángulo, criterios de divisibilidad, algoritmos para calcular los restos de las divisiones, etc.
Analizaré ahora algunas relaciones que existen entre los números de las columnas centrales del triángulo aritmético, lo que yo denomino la columna vertebral del mencionado triángulo, y en la que he encontrado dos propiedades muy importantes:
- Si dividimos la suma de cada fila por el valor central, en el caso de las filas de orden par, o por uno de los dos números centrales, en el case de las filas de orden impar, obtenemos valores que tienden a:
- Si dividimos la suma de cada fila por el valor central, en el caso de las filas de orden par, o por uno de los dos números centrales, en el case de las filas de orden impar, obtenemos valores que tienden a:
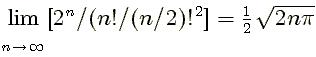
Sí, increíblemente nos hallamos con el número p presente en el triángulo aritmético, a partir de una simple división de dos valores enteros como son la suma de cada fila y la cifra central. ¡¡Maravillas insondables de las matemáticas!!
- Si nos fijamos sólo en los valores centrales de las filas de orden par y hacemos las sucesivas divisiones entre cada término y su anterior, comenzando desde el extremo superior, observaremos que estos cocientes aumentan progresivamente y tienden a un valor finito.
Pues bien, calculando el límite cuando el orden de las filas tiende a infinito obtenemos que la razón tiende a 4.
Si os interesa os ofrezco la demostración de esta propiedad.
Las filas de orden impar tienen dos valores centrales idénticos que, por tanto, generan un valor doble que es, precisamente, el número central de las filas de orden par. Este es siempre mayor que sus dos vecinos, pero que cuando avanzamos hacia a las filas de orden infinito, los valores centrales tienden a igualarse dando lugar a un aumento progresivo de las divisiones.
Si el salto de las filas de orden impar a par tiene por razón 2, las otras también tienden a 2 y, entonces, la razón del salto entre dos filas pares consecutivas tiende a 2 por 2, o sea, a 4.
Los números triangulares se generan geométricamente formando triángulos con aristas que aumenten progresivamente su número de puntos, un ejemplo fácil de imaginar es formar triángulos con monedas o con bolas situadas una encima de la otra.
Así necesitaríamos 1 bola para formar un triángulo de una sola fila, 3 para uno de dos filas, 6 para uno de tres filas, 10 para uno de cuatro, etc.
El algoritmo que genera estos números triangulares es: an = n · (n + 1) / 2
Los Pitagóricos adoraban los números triangulares, incluso, antiguamente tenían un cierto valor místico.
Tienen muchas y muy curiosas propiedades, veamos varias antes de volver al tema:
· Cada número al cuadrado es igual a ocho veces un número triangular más 1.
· Todo número triangular se puede expresar como la suma de tres números triangulares. (Gauss)
· Es posible hallar una infinitud de números triangulares que multiplicados entre sí, su resultado
sea un número al cuadrado., etc.
Así necesitaríamos 1 bola para formar un triángulo de una sola fila, 3 para uno de dos filas, 6 para uno de tres filas, 10 para uno de cuatro, etc.
El algoritmo que genera estos números triangulares es: an = n · (n + 1) / 2
Los Pitagóricos adoraban los números triangulares, incluso, antiguamente tenían un cierto valor místico.
Tienen muchas y muy curiosas propiedades, veamos varias antes de volver al tema:
· Cada número al cuadrado es igual a ocho veces un número triangular más 1.
· Todo número triangular se puede expresar como la suma de tres números triangulares. (Gauss)
· Es posible hallar una infinitud de números triangulares que multiplicados entre sí, su resultado
sea un número al cuadrado., etc.
Son los números generados, geométricamente, al formar hexágonos contenidos progresivamente unos dentro de los otros. El número de puntos necesarios para formarlos son los números hexamórficos.
El algoritmo que permite calcularlos es: H(n) = n · (2n - 1)
La serie obtenida es: 1, 6, 15, 28, 45, 66, 91, 120, etc.
Imaginemos un hexágono de 6 puntos, uno por arista, dentro de uno mayor de 2 puntos por arista (comparten algunos puntos en común) contenido en el interior de uno de 3 puntos por arista, etc.
El algoritmo que permite calcularlos es: H(n) = n · (2n - 1)
La serie obtenida es: 1, 6, 15, 28, 45, 66, 91, 120, etc.
Imaginemos un hexágono de 6 puntos, uno por arista, dentro de uno mayor de 2 puntos por arista (comparten algunos puntos en común) contenido en el interior de uno de 3 puntos por arista, etc.
Leonardo de Pisa, hijo de Bonacci, y más conocido por Fibonacci, matemático del siglo XIII publicó la serie numérica que lleva su nombre y que, comenzando por 1, 1, se genera sumando los dos números anteriores de la serie:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4081, 6665, 10746
DEMOSTRACIÓN de los TRIÁNGULOS GENERADOS por NÚMEROS PRIMOS
Si utilizamos la expresión general de las diversas cifras del triángulo aritmético en función de los números combinatorios veremos más clara esta cuestión.
Cada término del triángulo se puede expresar como el resultado del número combinatorio:
Cada término del triángulo se puede expresar como el resultado del número combinatorio:
Cuando hablamos de las filas de los números primeros, la n representa esta cifra y sabemos, en este caso, que no es divisible por ningún factor del denominador, (sólo por ny por 1).
Teniendo en cuenta que el resultado de los números combinatorios es siempre un número natural, deducimos que el denominador (m – n)! · m! ha de ser divisor de (n - 1)!, dado que de n no puede serlo, por tratarse de un número primero, para todos los valores de m , es a decir, tota la fila completa.
Esto implica que (n - 1)! / (m – n)! · m! = p ( dónde p es un valor entero necesariamente)
Por tanto, y dado que n! = n·(n - 1)!, obtenemos que n! / (m – n)! · m! = p·n
O sea, todos los números de una fila n, dónde n es un número primero, son múltiples de este número primero. Y todos los valores inferiores del triángulo generados por la suma de dos múltiples de n también lo serán, la cual genera el triángulo invertido de los números primeros dentro del triángulo.
Para hacer esta demostración expresaré los valores de la diagonal en forma de números combinatorios (n sobre m), la cual me permitirá operar y simplificar rápidamente.
Observamos que en esta diagonal para cada valor n, tenemos que m = n – 3, por ejemplo,
el 4 es n = 4, m = 1, el 10 es n = 5, m = 2, o el 20 es n = 6, m = 3, etc.
Si restamos dos términos de esta diagonal separados por dos saltos y expresados en forma de números combinatorios, obtenemos:
Observamos que en esta diagonal para cada valor n, tenemos que m = n – 3, por ejemplo,
el 4 es n = 4, m = 1, el 10 es n = 5, m = 2, o el 20 es n = 6, m = 3, etc.
Si restamos dos términos de esta diagonal separados por dos saltos y expresados en forma de números combinatorios, obtenemos:
Operando el numerador queda: n·(n2 + 3n + 2) – [n(n2 - 3n + 2)] = n · 6n = 6n2
Dado que 3! = 6, entonces queda 6n2 / 6 = n2
en la QUINTA DIAGONAL del TRIÁNGULO ARITMÉTICO
Como hemos visto en el capítulo sobre los cuadrados mágicos, el algoritmo para obtener la suma mágica S(x) de files, columnas y diagonales de un cuadrado mágico de orden n, compuesto por n2 números naturales, es:
Para hacer esta demostración expresaré los valores de la diagonal en forma de números combinatorios (n sobre m), la cual me permitirá operar y simplificar rápidamente.
Observemos que en esta diagonal para cada valor n, tenemos que m = n – 4, por ejemplo, el 5 es n = 5, m = 1, el 15 es n = 6, m = 2, o el 35 es n = 7, m = 3, etc.
Si restamos dos términos de esta diagonal separados por tres lugares o saltos obtendremos:
Observemos que en esta diagonal para cada valor n, tenemos que m = n – 4, por ejemplo, el 5 es n = 5, m = 1, el 15 es n = 6, m = 2, o el 35 es n = 7, m = 3, etc.
Si restamos dos términos de esta diagonal separados por tres lugares o saltos obtendremos:
Operando el numerador: n·(n3 + 6n2 + 11n + 6) – [n·(n3 - 6n2 + 11n - 6)] = n(12n2 + 12)
como que 4! = 24, el resultado del cociente será:
n·(n2 + 1) / 2
Resultado que coincide con el algoritmo de la suma mágica.
Los valores centrales de un fila n cualquiera ocupen el lugar n / 2, para simplificar la demostración asignaré al número de fila el valor 2n i, por tanto, al término central la posición n.
La razón entre los dos números centrales de dos filas de orden par consecutivas, en forma de números combinatorios, es:
La razón entre los dos números centrales de dos filas de orden par consecutivas, en forma de números combinatorios, es:
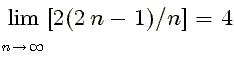
Suscribirse a:
Comentarios (Atom)
Archivo del blog
-
►
2017
(19)
- ► septiembre (1)
-
▼
2014
(441)
- ► septiembre (61)
-
►
2011
(38)
- ► septiembre (4)
-
►
2010
(74)
- ► septiembre (6)
