| A | B | C | D |
| 5 | 4 | 3 | 2 |
| 5 | 4 | 3 | 2 |
| 5 | 4 | 3 | 2 |
| 1 | 4 | 3 | 2 |
| 1 | 0 | 3 | 6 |
| 1 | 0 | 3 | 6 |
- El dado A gana al B en 24 de cada 36 tiradas.
- El dado B gana al C en 24 de cada 36 tiradas.
- El dado C gana al D en 24 de cada 36 tiradas.
Se puede establecer un orden de mejor a peor, que es:
A mejor que B mejor que C mejor que D. El jugador que escoge en primer lugar tiene, pues, una ventaja que, para que el juego sea equitativo, debe compensar con un pago inicial. Si prevé jugar 36 partidas, ¿cuál ha de ser este pago?
A mejor que B mejor que C mejor que D. El jugador que escoge en primer lugar tiene, pues, una ventaja que, para que el juego sea equitativo, debe compensar con un pago inicial. Si prevé jugar 36 partidas, ¿cuál ha de ser este pago?
2. Alicia, Bernardo y Carlos están en línea recta. Alicia está a un metro de Bernardo, David está a un metro tanto de Bernardo como de Carlos y Alicia está a la misma distancia de Carlos que de David. ¿A qué distancia está Carlos de Bernardo?
3.Probar que todo número racional positivo se puede expresar como suma de fracciones de numerador unitario y denominadores enteros positivos todos distintos.
4.
SOLUCIONES
1.El problema es ilusorio. Basta con comparar y se comprobará que el dado D gana también al A en 24 de cada 36 ocasiones. La asunción implícita de que el concepto mejor que es transitivo debe descartarse.
Un análisis más a fondo demuestra que la simetría entre los dados dos a dos no se extiende al total. El dado A que, según hemos visto, gana al B y pierde con el D, empata con el C. El dado B, que pierde con el A y gana al C, pierde por poco con el D.
Si se echaran simultáneamente los 4 dados, no ganarían todos por igual en las 1296 combinaciones posibles:
- A gana 432 veces.
- B gana 288 veces.
- C gana 144 veces.
- D gana 432 veces.
- ABC: A=108, B=72, C=36
- ABC: A=72, B=48, C=96
- ACD: A=72, C=72, D=72 (Único caso simétrico)
- BCD: B=96, C=48, D=72
2. Hay dos soluciones, según Carlos esté más alejado o más próximo a Alicia.
Primera solución
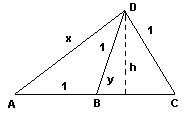
AB = 1; DB = 1; DC = 1; AD = AC = x; BH = y; DH = h AHD x² = (1+y)² + h² DHB 1 = y² + h² AD = AC x = 1 + 2y Resolviendo y = (-1+5½)/4 = 0.618 m (aprox)Segunda solución
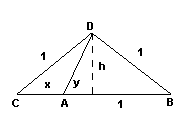
AHD x² = y² + h² DHC 1 = (x+y)² + h² DHB 1 = (1-y)² + h² Resolviendo x = (-1+5½)/2 = 1.618 m (aprox)
3. Sea r = p0 / q0 (p0 y q0 enteros) el número racional elegido. Tomamos a0 como el mínimo entero positivo tal que (1/a0)<=(p0/q0), y ponemos p1/q1 = p0/q0 -1/a0 = (p0a0-q0)/a0q0, es decir, p1=p0a0-q0. En las siguientes etapas, se toma an como el mínimo entero positivo no usado con anterioridad, tal que 1/an<=pn/qn, y ponemos p(n+1) = pnan-qn, q(n+1)=anqn, de modo que p(n+1)/q(n+1) = pn/qn - 1/an.
Si en determinada etapa fuese p(n+1) = 0, el proceso terminaría y tendríamos que r = 1/a0 + 1/a1 + 1/a2 + ... + 1/an. Veremos que esto es precisamente lo que sucede, ya que la serie no puede proseguir indefinidamente.
Cada denominador an (n>=1) es de una de estas dos clases:
1) an = a(n-1) + 1 , o bien
2) an > a(n-1) + 1, en cuyo caso an es el mínimo entero positivo tal que 0 <= pnan - qn. Esto implica que p(n+1) = pnan-qn < qn, pues de lo contrario sería 0 <= pn(an - 1 ) - qn y entonces an no sería mínimo.
Si todos los denominadores fuesen de la primera clase, la serie no podría proseguir indefinidamente porque la serie armónica 1 + 1/2 + 1/3 + ... es divergente. Si algún denominador fuera de la segunda clase, entonces todos los que le siguen también lo son.
En efecto: 1/(an - 1) > pn/qn = 1/an - p(n+1)/q(n+1) > 1/an + 1/a(n+1), luego 1/a(n+1) < 1/(an - 1) - 1/an, de donde a(n+1) > an(an -1) > = an + 1 . Puesto que esto implica que, a partir de ese punto será p(n+1)
4. A .Se trata de un concurso de belleza.
B .¿Quién ha dicho que era de noche?
C .Era un entierro.
D. El desconocido tenía hipo.
B .¿Quién ha dicho que era de noche?
C .Era un entierro.
D. El desconocido tenía hipo.
TOMADO DE: http://www.mensa.es/juegosmensa/e046050.html
