
Vamos a obtener matrices escalonadas porque sabemos que si una fila solamente contiene ceros será linealmente dependiente.
Para obtener una matriz escalonada el elemento (2 1), es decir, el 4 lo hemos de convertir en 0 y para ello, multiplicamos a los valores de la F 1 (fila 1) por 4 y vamos restando a los valores de F2 (fila 2) tal como queda indicado más abajo:
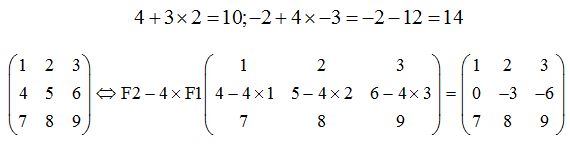
Siguiendo con la construcción de una matriz escalonada, el elemento que se halla en la posición (3 1) que es el 7 también ha de ser igual a cero y para ello multiplicamos a los valores de la fila 1 (F1) por -7 y vamos restando de los valores de F2:
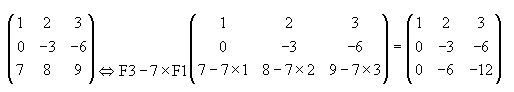
Recuerda que tratamos de obtener una matriz escalonada. En este momento el valor situado en (3 2), -6 ha de ser cero por lo que debo dirigirme a
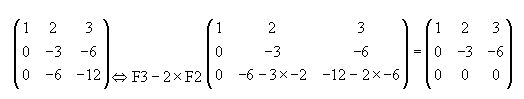
Observo que tengo dos filas linealmente independientes o dos filas que no son ceros, luego el rango vale 2.
Ejercicio #30
Calcula el rango de la matriz: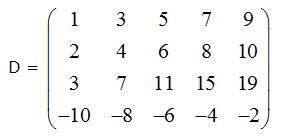
Respuesta: rang (D) = 2
Solución
Siempre has de tratar de conseguir que el primer elemento de la 2ª fila (2 1) sea 0. Seguidamente, el (3 1) también, y así hasta lograr que a partir de la 2ª fila, los elementos de la 1ª columna sean ceros.
Una vez que lo hayas conseguido y si ves que todavía no sabes el rango de la matriz, debes tratar que el 2º elemento de la 3ª fila sea cero, es decir, tratar de obtener una matriz escalonada.
En cuanto veas que la última o últimas filas completas sus elementos son iguales a cero has terminado con el cálculo. Cuantas las filas independientes y ya tienes su rango.
Esto es lo que ves a continuación paso a paso: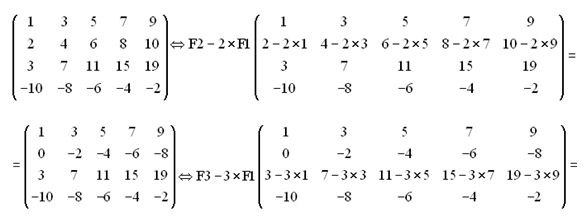
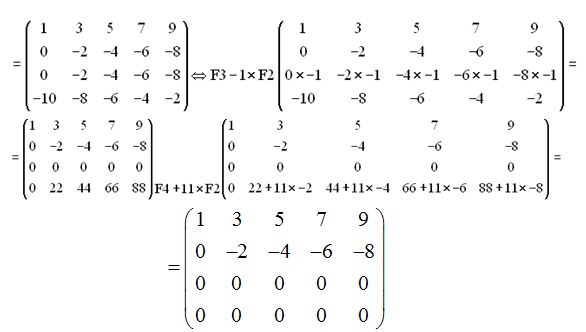
Vemos que dos filas son linealmente independientes, luego el rango de esta matriz es 2.
Ejercicio #31
Calcula el rango de la matriz siguiente: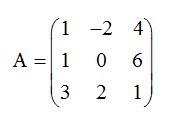 Respuesta: r(A) vale 3
Respuesta: r(A) vale 3tomado de: http://www.aulafacil.com/matematicas-matrices-determinantes/curso/Lecc-14.htm

No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.