Historia del método del límite

¿cuándo surge por primera vez el método del límite? ¿ qué problemas trataba de resolver?
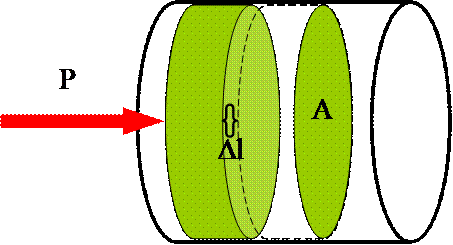
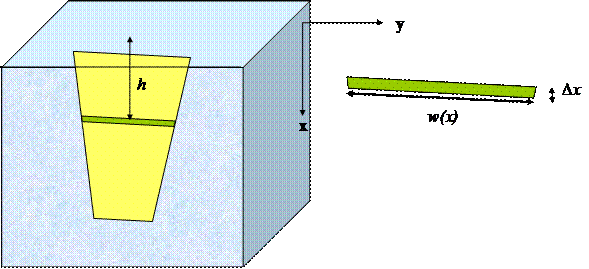
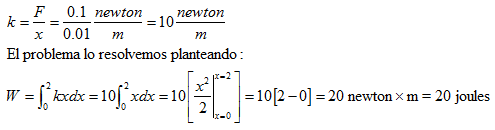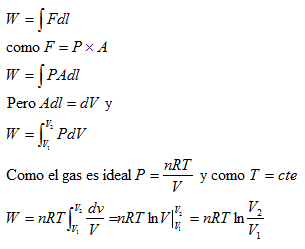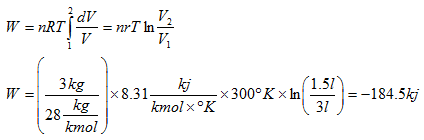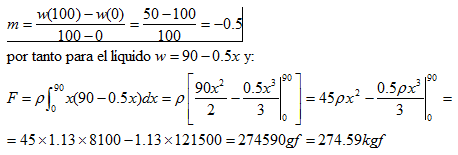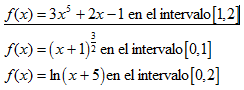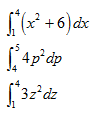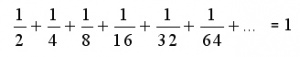Como la mayoría de los conceptos y métodos matemáticos ( así como las principales cuestiones filosóficas y de interés vital que se ha planteado la humanidad), nos debemos remontar a los griegos de la antigüedad.

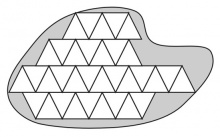
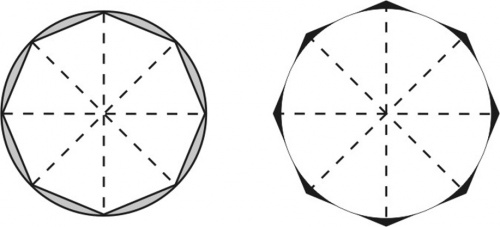
En el siglo V a.c. se atribuye al sofista Antifonte el primer intento por calcular la cuadratura del círculo. Éste inscribe un cuadrado en el círculo.

En cada segmento circular formado, inscribe un triángulo isósceles, y va repitiendo este proceso sucesivamente de modo que “en algún momento se agotaría el círculo, inscribiendo de ese modo un polígono cuyos lados, por su pequeñez, coincidirán con la circunferencia. Y dado que podemos cuadrar cualquier polígono, estaríamos en disposición de construir un cuadrado igual al círculo”.
Este primer intento de cuadratura adolece de falta de rigor, pero Antifonte ya considera una sucesión de polígonos inscritos que tienden a agotar el círculo. Sin embargo, no ofrece ningún criterio riguroso para razonar por qué se va a agotar el círculo en este proceso.
Un siglo más tarde Eudoxo retoma esta cuestión y , en su línea habitual de trabajo serio y profundo, aporta el rigor suficiente para responder a este interrogante y fundamentar un método que posteriormente en el siglo XVII será denominado de exhausción. Eudoxo se basa en el siguiente lema:
“Si se ponen dos magnitudes desiguales y de la mayor se quita una magnitud mayor que su mitad, y de la restante se quita una magnitud mayor que su mitad y así sucesivamente, quedará una magnitud que será menor que la magnitud menor dada”
Eudoxo tiene por primera vez la genialidad de evaluar con un criterio claro y nítido cuándo una magnitud tiende a anularse : cuando en el proceso llega a valer menos que cualquier otra magnitud dada.
Si partimos de una magnitud M , y la sometemos a un proceso como el anterior de eliminar sucesivamente una parte mayor que su mitad , ¿ llegará a valer menos que una cantidad cualquiera C?
Después del primer paso, M se habrá convertido en M-rM = M*(1-r),      (1/2)Después del segundo paso, se habrá convertido en M*(1-r) – M*(1-r)*r = M*(1-r)^2
...............
Después del paso n-ésimo , se habrá convertido en M* (1-r)^n
¿ Para algún valor de n, conseguiremos que M*(1-r)^n < C ?
Tomando logaritmos neperianos en esta expresión y despejando n, obtenemos que n > (lnC-lnN)/ln(1-r).
Luego basta con aplicar un número de pasos n, superior a este cociente , para asegurarnos que M se ha convertido en un valor inferior a C.
En este razonamiento realizado con terminología actual se observa que no es necesario que eliminemos en cada paso más de la mitad de la magnitud, como indica Eudoxo. No es necesario que r>(1/2). Basta simplemente que 0
Con este criterio de Eudoxo sí se puede garantizar que los polígonos mencionados de Antifonte agotan todo el círculo, pues , como se ve fácilmente en la figura, el área del triángulo quitado en cada segmento circular es mayor que la mitad del área de éste.

En efecto, consideremos un rectángulo, trazando la tangente por el punto medio del segmento. El área del triángulo es la mitad del rectángulo; pero este rectángulo tiene mayor área que el segmento. Luego, el área del triángulo es mayor que la mitad del segmento circular.

 

Aunque la exigencia de Eudoxo de eliminar en cada paso más de la mitad no sea necesaria, su razonamiento es impecable y genial. Descubre un criterio para demostrar cuándo una sucesión de polígonos tendrá como límite una figura ( “agotará esa figura”).
Arquímedes utiliza este método establecido por Eudoxo para cuadrar un segmento de parábola. Aporta otra novedad: además de inscribir polígonos , circunscribe otra sucesión de polígonos; de este modo, consigue que la diferencia entre los polígonos circunscritos e inscritos sea menor que cualquier número dado. El método de “exhausción” se ha transformado en el método de “ compresión” ; la figura queda comprimida entre ambas sucesiones de polígonos.
Aunque los griegos nunca utilizaron la palabra límite, hemos visto cómo Eudoxo y Arquímedes conocieron y usaron las ideas principales que configuran este método. Sin embargo no disponían de un simbolismo adecuado algebraico que facilitara su definición y, por otra parte, su planteamiento se limitaba sólo a figuras geométricas.
Hubo de esperar muchos siglos para que estas ideas fecundas de los griegos fructificaran. En el siglo XVI I, con motivo del estudio del movimiento iniciado antes por Galileo, algunos matemáticos insignes como Fermat, Descartes, Newton y Leibniz empezaron a vislumbrar las posibilidades del método de los límites.
Posteriormente en el siglo XVIII Euler consiguió relacionar todas las ideas y métodos de sus predecesores y englobarlos en una teoría más general que desde entonces se llama análisis infinitesimal, análisis de los procesos infinitos. Por último Cauchy definió por fin el concepto de límite tal y como actualmente se estudia en cualquier centro de enseñanza.

TOMADO DE:http://www.jpimentel.com/departamentos/matematicas/nanagonza/limite.htm

Estiramiento de un muelle

Analicemos ahora un último ejemplo , extraído de la física, que se resuelve de forma sencilla con la estrategia del límite.
La mayoría de las fuerzas que actúan en la naturaleza son variables, no permanecen constantes : así, al estirar un muelle , el esfuerzo de alargarlo el primer decímetro es menor que el del segundo decímetro. Cuanto más estirado está el muelle, más fuerza tenemos que emplear para mantenerlo en dicha posición.La fuerza que tiende a recuperar su posición es cada vez mayor, de modo proporcional a la longitud estirada ( F = -kx , la constante k depende de cada muelle). Cuanto más estirado está el muelle, más nos cuesta alargarlo. La constante k depende de cada muelle.

¿Cómo calcular el trabajo que se emplea para estirar un muelle ,de constante k, una longitud L ?

Sabemos que el trabajo es el producto escalar de la fuerza que actúa sobre unn objeto por sudesplazamiento . Pero en nuestro caso la fuerza es variable, como hemos indicado antes. ¿Qué valor asignamos a la fuerza durante todo el proceso de alargamiento? ¿La que actúa al principio del proceso? ¿La que actúa en un punto intermedio?
Está claro que en todos estos casos cometemos un error significativo. La estrategia del límite nos da la solución de nuevo a este problema....
Dividimos en 4 partes iguales el desplazamiento y suponemos que la fuerza es constante en cada una de éstas, eligiendo en cada intervalo la fuerza que actúa en su extremo derecha:

Con estas hipótesis ¿ cuál es el trabajo para estirar la longitud L ?
En el primer tramo la fuerza F= -k* L/4,y el desplazamiento es L/4. El trabajo es , por tanto, -k*L/4 *L/4 = -k*L^2/4^2.

En el segundo tramo, el trabajo es -k*(2L)/4*L/4

..............
El trabajo total es la suma de estos trabajos : -k*(L^2/4^2) *(1+2+3+4)

Como antes, si ahora dividimos el trayecto en 8 partes , la aproximación al valor buscado es mejor:

-k*(L^2/8^2)*(1+2+....+8)

Por último, dividiendo el trayecto en n partes,

-k*(L^2/n^2)*(1+2+.....+n)= -k*(L^2/2)*(1+1/n)

El trabajo total es el límite de esta expresión cuando el número n de intervalos iguales tienda a ( de esta forma, la longitud de cada intervalo es infinitamente pequeña y no hay error al considerar constante la fuerza en él).

Por tanto, el trabajo de estirar el muelle de constante k una longitud L es
-k*(L^2)/2

El límite y los infinitésimos

El método del límite proporciona un modo de fundamentar con rigor el cálculo diferencial sin recurrir a los infinitésimos , que , aunque eficaces en la resolución de problemas, resultaban conceptos muy oscuros y difusos tal y como los concibieron inicialmente Newton y Leibniz.
Supongamos que un coche parte del reposo y alcanza una velocidad de 110 km/h. Está claro , por la continuidad de la velocidad, que al menos en un instante este coche iba a 100 Km/h, según marcaba su cronómetro. Esta velocidad no es una cuestión simplemente teórica , sino que tiene un significado real y práctico: si el coche en ese instante tuviera un accidente, sus consecuencia dependen de esta velocidad. Del mismo modo, el alcance y altura de un proyectil lanzado por un cañón depende de la velocidad instantánea de salida por el tubo de éste.
Pero analicemos detenidamente este concepto que en principio parece evidente y sencillo. ¿Qué significa que en un instante la velocidad es de 100 Km/h? Suponemos que el coche no se ha mantenido con esa velocidad durante una hora en la que habría recorrido 100 kms. Está claro que para el cálculo de la velocidad no necesitamos que el coche esté en marcha durante una hora. Si la velocidad es constante, es suficiente con medir la distancia recorrida durante un tiempo determinado y calcular el cociente de esta distancia entre el tiempo empleado.
Si la velocidad no se ha mantenido constante en ningún período de tiempo ¿ cómo calcular ésta en un instante dado, que es distinta a la de un instante anterior y posterior? Si el tiempo de un instante es 0, también lo es la distancia recorrida en ese tiempo.¿Cómo calcular entonces la velocidad instantánea como un cociente 0/0?
Newton y Leibniz suponen la existencia de cantidades muy pequeñas, próximas a 0, a las que denominan infinitésimos, que aparecen y se desvanecen en el cálculo de su cociente, que sí es distinto de 0. Se trata evidentemente de un proceso nada riguroso: se sacan de la manga cantidades que apenas se diferencian de 0 y después desaparecen cuando han cumplido su misión como numerador o denominador. Sin embargo, los resultados obtenidos por estos dos grandes matemáticos no eran nada triviales y solucionaban problemas que durante siglos habían permanecido sin ser resueltos ( cálculo de velocidades, de máximos y mínimos, de cálculo de tangentes a curvas,...).
La estrategia del límite resuelve esta dificultad sin recurrir a los difusos infinitésimos. La noción de límite se aplica a distancias y tiempos pequeños, pero no infinitesimales.
Si conocemos el espacio recorrido en cada período de tiempo, calculamos las velocidades del coche en los intervalos previos al instante t:
(t -1,t ), (t -1/2,t ), ......(t -1/n,t)).....
Estas velocidades forman una sucesión cuyo límite , cuando n se hace tan grande como se quiera, coincide con la velocidad v en el instante .
Si analizamos este ejemplo, observamos que el método del límite no sólo permite calcular algunos valores exactamente, sino que es además una herramienta adecuada para definir conceptos y magnitudes físicas. ¿Cómo, si no, podemos definir la velocidad instantánea?
Como veremos en los capítulos de la derivada e integral, la mayoría de los conceptos de la física se definen mediante la estrategia del límite.

TOMADO DE:http://www.jpimentel.com/departamentos/matematicas/nanagonza/limite.htm

El número e

Hablemos ahora de los intereses que produce una cantidad de dinero colocada en un banco. La práctica usual es que los intereses se contabilizan y acumulan al final de cada año.
Así, si se pone 1 euro al interés anual de i por unidad ¿En qué se convierte después de t años?
Durante el primer año, el euro se convierte en 1+i.Durante el segundo año, cada euro se convierte en 1+i. Como al principio de este año, había 1+i, éstos se convierten en (1+i)^2
Repitiendo este proceso , a los t años el euro inicial se ha convertido en (1+i)^t
Supongamos ahora que el interés anual es del 1 por unidad y los períodos de capitalización son los trimestres; es decir, los intereses generados en el primer trimestre se acumulan al capital para producir en adelante nuevos intereses, y así sucesivamente en cada trimestre. El interés por unidad en cada período es ahora i/4 y durante un año hay 4 períodos de acumulación. Por tanto, al cabo de un año 1 euro se habrá convertido en (1+i/4)^4.
Razonando análogamente, si el período de acumulación de intereses fuera un mes, entonces 1 euro se convierte al final de un año en (1+i/12)^12.
Si el período de acumulación fuera un día, entonces 1 euro se convierte al final de año en (1+i/360)^360.
Como cabía esperar , cuanto más breve es el período de acumulación , más beneficio produce el capital inicial
( antes empiezan los interesados generados a producir nuevos intereses ).
Siguiendo este razonamiento, surge de forma natural la siguiente pregunta ¿ Y si el período de acumulación es un instante ? es decir ¿ y si el interés desde el mismo instante en que es generado, empieza a su vez a generar nuevos intereses ? Estamos entonces ante lo que se llama un interés continuo. El concepto de instante y su relación con la idea de límite se analizarán con más profundidad en el capítulo de las derivadas.
La estrategia del límite nos da de nuevo la solución a este problema. Nos permite dar el salto de un proceso discreto a otro continuo. Buscamos un proceso en el que cada vez obtengamos aproximaciones mejores al valor buscado y además estas aproximaciones se acerquen al valor tanto como se quiera .
Si utilizamos n períodos iguales de acumulación durante el año, argumentando como antes , 1 euro se convierte al final del año en (1+1/n)^n.
Cuanto mayor sea n, menor será el período de acumulación, de modo que éste tenderá a 0 ( será un instante ) cuando n tienda a infinito.
Así, con un interés continuo del 100 %, 1 euro se convierte , al final de un año, en el valor  lim (1+1/n)^n . Sabemos que este límite es el número e. Su nombre se debe al gran matemático Euler, quien descubrió la relación existente entre los tres números más famosos de la matemática .
Si es famoso el número e, no es por el interés continuo , que nunca se da en la práctica habitual en los términos anteriores ( ninguna entidad financiera ofrece un interés continuo, y menos al 100 % anual ). Pero el interés continuo simboliza muy bien el modelo que siguen todos los procesos de crecimiento y decrecimiento continuos , tan frecuentes en la naturaleza.
El crecimiento de la masa forestal de un extenso bosque, el crecimiento de una colonia de insectos o virus, la desintegración radiactiva ,....son procesos continuos, en los que la acumulación o el decrecimiento se producen instantáneamente ( no hay un período de tiempo en el que los elementos generados permanecen inactivos esperando una señal para incorporarse al proceso , sino que ,desde el mismo instante en que son generados, participan como el resto en el proceso de crecimiento) . Por eso, en las ecuaciones que rigen estos modelos aparece siempre el número e

TOMADO DE:http://www.jpimentel.com/departamentos/matematicas/nanagonza/limite.htm

La estrategia del límite

Introducción

Vamos a hablar sobre un concepto clave en varias ramas importantes de la matemática: la estrategia del límite. Junto al de función, es la idea básica del “análisis ( o cálculo) infinitesimal”, que comprende tanto el estudio de la derivada como el de la integral.
A pesar de la importancia de este concepto ( o método), durante el Bachillerato no se llega a explicar suficientemente el significado ni el alcance de esta potente herramienta. Eso sí, los alumnos calculan límites con una gran pericia cuando se aprenden las distintas técnicas elementales, que parecen “extraídas de la manga”. Así, no se arrugan ante cálculos tan laboriosos como 
Incluso les gusta realizar estos cálculos que les resulta bastante sencillo, pero no llegan a entender para qué sirve calcular estos límites.
¿ Para qué necesitan calcular el límite de la función ? ¿ O el ? Los más aventajados calculan este último límite para hallar una asíntota oblicua de una función , pero ,además de esta aplicación, no encontrarán otro sentido a este límite.

No asimilan ( o no nos esforzamos los profesores porque lo asimilen) las ideas básicas que subyacen en estos cálculos. Algo parecido ocurre con otros conceptos o métodos matemáticos: el cálculo de las raíces cuadradas, de derivadas, de integrales ( los alumnos calculan con destreza hasta llegar a sus resultados, pero en general desconocen el significado y las aplicaciones de éstos, que es lo más importante ).

La mayoría de nuestros alumnos de Bachillerato no sabrían responder con cierto criterio a las siguientes preguntas: ¿ qué problemas prácticos resuelve el método de los límites? ¿ qué significa la expresión ? ¿cómo explicar con palabras sencillas el significado de que ? ¿ Por qué ?

Incluso me atrevo a indicar que muchos estudiantes universitarios de Ciencias tampoco sabrían responder a estas preguntas con cierta profundidad. Muchos estudiantes de Ingeniería calculan límites muy complicados, pero estoy convencido de que pocos de ellos tienen una idea clara de su contenido y alcance.
Es cierto que los conceptos matemáticos son más difíciles de asimilar que los métodos memorísticos de cálculo y van madurando en un proceso lento de varios años . Pero los profesores no debemos renunciar a explicar las ideas básicas que conforman los conceptos matemáticos importantes desde el primer momento en que los manejan nuestros alumnos.
Es mucho más fácil explicar el cálculo de un límite que el de razonar sobre su significado, pero no nos debemos limitar al simple cálculo y tenemos que esforzarnos para que nuestros alumnos desde el principio asimilen las ideas principales de este concepto, aunque en los primeros momentos les resulte difícil. Sin este esfuerzo, realizado a lo largo de varias etapas de maduración, nuestros alumnos no asimilarán la idea de límite, y no les habrá servido de nada su estudio durante tantos años.
Veamos con tres ejemplos sencillos el alcance y la estrategia del límite.
a) Trabajo de un motor

Para empezar, consideremos un recipiente cilíndrico de altura h y radio de la base R. Queremos extraer con un motor el agua que lo llena. ¿Qué trabajo realiza este motor para vaciar el recipiente?

Sabemos que el trabajo es el producto de una fuerza por un desplazamiento. En este caso, la fuerza es el peso del agua, y el desplazamiento es la altura que tiene que subir el agua hasta el nivel superior del recipiente, antes de sacarla de éste.
Pero aquí surge el problema : esta altura es diferente para cada capa de agua. El agua que está en el fondo hay que elevarla una altura mayor que la que se encuentra en la mitad del recipiente. El desplazamiento de cada capa de agua es diferente, varía según la altura de dicha capa dentro del recipiente.
Si consideramos el recipiente descompuesto en 8 capas y suponemos que la altura del agua en cada capa es igual (lo cual evidentemente no es cierto), al sumar el trabajo de elevar estas 8 capas no obtenemos el valor exacto, pero sí una aproximación a este trabajo.
Como la densidad del agua es 1000 kg/m3 , el peso de la capa superior es . Suponiendo que toda esta capa se eleva h/8, el trabajo efectuado por el motor es 
Del mismo modo , el trabajo del motor para elevar la segunda capa es 
Así , el trabajo total del motor para elevar las 8 capas es : 
¿Cómo podemos mejorar este cálculo para aproximarnos más al valor exacto del trabajo?
Si en vez de 8 capas, consideramos 16 de igual altura, el error de considerar que todo el agua de una misma lámina está a la misma altura es evidentemente menor que antes. Este trabajo es .
Si sucesivamente vamos considerando 32 capas, 64,..... obtenemos una sucesión de valores, en la que cada término se aproxima más al valor buscado.
Si dividimos el recipiente en n capas de igual altura, el trabajo es 
= 
Si n aumenta , el cociente 1/n disminuye hasta casi anularse , lo mismo que la altura h/n de cada lámina . De este modo , el error que hemos cometido al considerar que todo el agua de cada lámina se encontraba a la misma altura, se puede hacer tan pequeño como queramos siempre que el espesor de cada capa sea suficientemente pequeño. El trabajo realizado por el motor es la tendencia ( el límite ) de la expresión anterior al aumentar n indefinidamente. Su valor exacto es kilográmetros, si R y h están expresados en ms.
Reflexionemos sobre este proceso que hemos seguido. Se trata de un razonamiento teórico en el que hemos sustituido el movimiento continuo de extracción del agua por el discreto de considerar el agua compuesta por capas . Evidentemente este proceso no refleja la exactitud del proceso físico que se sigue en la realidad. Pero hemos conseguido una sucesión de aproximaciones en la que cada término se ajusta más al proceso real, de modo que en el límite esta aproximación se acerca al valor buscado tanto como se quiera.
El método del límite consiste , por tanto, fundamentalmente en que para determinar el valor de una magnitud, se sigue un proceso en el que se van calculando aproximaciones al valor buscado. En este proceso se debe asegurar que cada aproximación debe mejorar la aproximación anterior.
Del estudio de este proceso, se observa la tendencia de sus aproximaciones sucesivas y se calcula el valor al que tienden éstas. Pero para asegurarnos que éste es el valor buscado, debemos garantizar que la diferencia entre éste y las sucesivas aproximaciones se puede hacer tan pequeña como se quiera.
Por tanto, la estrategia del límite incluye tres pasos:
1) Se construye un proceso de aproximaciones al valor buscado.
2) Se calcula el valor al que tienden estas aproximaciones.
3) Se garantiza que las aproximaciones se acercan al valor anterior tanto como se quiera.

Veamos ahora cómo este método permite definir de un modo natural el número e. La mayoría de los libros de texto inician el estudio de este número sacándose de la chistera la sucesión que le origina, para terminar expresando que e es la base de los logaritmos naturales ( pues si no llega a ser natural...).

TOMADO DE: http://www.jpimentel.com/departamentos/matematicas/nanagonza/limite.htm

Aplicaciones de la integral definida

Aplicaciones de la integral definida

Hasta ahora hemos visto el cálculo de las integrales. Ahora veremos que la integral definida es un método rápido para calcular áreas, volúmenes, longitudes, etc., con gran aplicación en diversas ramas de las ciencias naturales, sociales y la ingeniería. Abordaremos algunas de las más importantes de acuerdo a su plan de estudios.

Determinación del trabajo

Si una fuerza constante F actúa sobre un objeto desplazándolo una distancia x, a lo largo de una línea recta, y la dirección de la fuerza coincide con la del movimiento, entonces el trabajo realizado W se expresa como el producto de la fuerza F por el camino recorrido, es decir:

W = F× x

Sin embargo, cuando la fuerza no es constante, por ejemplo, cuando se contrae o estira un resorte, el trabajo no se puede expresar en forma tan simple, pues la fuerza dependerá de la posición que ocupe el objeto sobre el cual actúa. Si conocemos la función que relaciona a la fuerza con la posición, F = f(x) (dejando para su estudio personal el planteamiento formal de dividir el intervalo en que actúa la fuerza en segmentos, etc.), podemos plantear entonces que:

El alargamiento o la compresión de un resorte helicoidal, nos proporciona un ejemplo del trabajo realizado por una fuerza variable. La ley de Hooke indica que la fuerza necesaria para estirar un resorte helicoidal, es proporcional a la elongación del resorte. Así, la fuerza necesaria para producir una elongación de x unidades, está dada por la expresión F = kx, donde k es la constante de proporcionalidad, que depende del material, del calibre (grosor), del alambre, de la temperatura, etc.

Ejemplo: Para producir una elongación de 0.01 m en un resorte de hacer se necesita aplicar una fuerza de 0.1 newton. Determine el trabajo necesario para comprimir el resorte 2 cm.

La determinación de la constante en la ley de Hooke se reduce a:

Nos interesa abordar con Ustedes el trabajo relacionado con la compresión o expansión de un gas en un cilindro con un pistón. Esto se relaciona, por ejemplo, con el trabajo que se realiza en los motores térmicos de combustión interna (motores de gasolina, motores diesel), o sea con el trabajo que realizan los gases calientes, productos de la combustión, sobre el émbolo del pistón que mueve al cigüeñal y, mediante los mecanismos de transmisión, mueven en definitiva las ruedas de un vehículo u otras partes mecánicas que nos dan un trabajo e una aplicación en la tecnología. Esto será visto en termodinámica, por lo que consideraremos un caso sencillo en este momento.

Supongamos que tenemos un gas ideal en un cilindro como el que se muestra en la siguiente figura y que es comprimido utilizando una presión P, manteniendo la temperatura constante:

Consideremos un desplazamiento muy pequeño del pistón, Dl, que en el límite será muy pequeño e igual a dl, para la ecuación del trabajo ya vista tendremos que:

Ejemplo. Asumiendo comportamiento ideal, determine el trabajo necesario para comprimir 3 kg de nitrógeno de 3 a 1.5 l.

Ya se verá en termodinámica que el signo negativo que se obtiene indica que el trabajo se realiza sobre el sistema.

Determinación de fuerza hidrostática.

Otra aplicación de la integral definida de aplicación en problemas de la Tecnología de Alimentos, consiste en determinar la fuerza ejercida por la presión de un líquido sobre una placa sumergida en él o sobre un lado del recipiente que lo contiene.

La presión de un líquido es la fuerza por unidad cuadrada de área ejercida por el peso del líquido. Así, si r es la densidad del líquido, entonces la presión ejercida por el líquido en un punto a h unidades debajo de la superficie del líquido es P unidades, donde  P  =  r× h.

El principio de Pascal establece que la presión a una profundidad h es la misma en todas las direcciones. Por tanto, si se sumerge una placa plana en un fluido de densidad ρ, la presión sobre un lado de la placa es ρ×h en cualquier punto. Resulta irrelevante si la placa se sumerge horizontal, vertical o de cualquier otro modo.

Consideremos una placa de forma irregular (por facilidad en el dibujo le dimos forma trapezoidal), sumergida en un líquido de densidad r, y cuyo ancho es función de la profundidad, dado por w(x). La orientación del eje x por conveniencia la consideramos con el origen en la superficie del líquido (ver la figura que sigue).

Consideremos un elemento muy pequeño y transversal de la placa. En el límite, cuando Dx sea infinitamente pequeño, su área será w(x)×dx, y podemos aproximar la presión ejercida por el líquido sobre ese elemento por el de uno similar pero orientado horizontalmente, ya que dx es infinitamente pequeño, que será ρ×x y por tanto la fuerza ejercida en ese diferencial de área por el líquido será dF = PdA = ρx w(x)dx. Evidentemente, integrando entre la profundidad del extremo superior de la placa y la profundidad del extremo inferior de la placa tendremos la fuerza total que se ejerce sobre la misma:

Ejemplo. 

Un recipiente de forma trapezoidal de 100 cm de profundidad, está lleno de un líquido viscoso cuya densidad es de 1.13 g/cm³. En la superficie el ancho del recipiente es de 100 cm y en el fondo es de 50 cm. Si la superficie del líquido se encuentra a 10 cm del borde del recipiente, determine la fuerza total ejercida por el líquido sobre una pared del recipiente.

La anchura es una función lineal de la profundidad, con w(0) = 100 y w(100) = 50.

La pendiente es:

Ejercicio:

Se tiene un depósito cilíndrico horizontal de 4 m de diámetro lleno exactamente en un 50 % con agua. Determine la fuerza hidrostática sobre las paredes laterales del cilindro.

Pista: Recuerde que resolviendo para y la ecuación de una semicircunferencia se tiene que:

Longitud de un arco.

El problema general que vamos a plantearnos es el cálculo de la longitud de arco de la curva y = f(x) en el intervalo [a, b]. Suponemos que f es continua en [a, b] y derivable en (a, b).

Haciendo una partición del intervalo [a, b] en n subintervalos de igual longitud: a = x₀ < x₁ < … < x_n = b, donde

Entre cada par de puntos consecutivos de la curva, (x_i–1, f (x_i–1)) y (x_i, f (x_i)), aproximamos la longitud de arco s_i por la distancia recta entre ellos (vea la figura). Aplicando la fórmula de la distancia entre dos puntos:

Este resultado lo puede comprobar utilizando GraphicaMK (materiales auxiliares), utilizando la función (1+4x^2)^0.5 e integrando entre 1 y 2.

Igual resultado se puede obtener integrando en y. Si la función g y su derivada g´ son continuas en el intervalo cerrado [c,d], entonces la longitud del arco de la curva x = g(y) a partir del punto (g( c ),c) hasta el punto (g(d),d) está dada por:

Ejercicio: Determine la longitud del arco de la curva y = x^2/3 desde el punto (1,1) hasta el punto (8,4). Respuesta: 7.634.

Otras aplicaciones de la integral definida.

Además de la determinación de áreas planas, las integrales definidas tienen otras aplicaciones que exceden lo previsto para este curso. Las mismas están relacionadas con el cálculo de áreas y volúmenes de revolución. No obstante se les remite a un material sobre las mismas (tomado de http://www.satd.uma.es/matap/javi/Calit/Temas/T5.pdf) y a la bibliografía disponible en la biblioteca.

Tarea:

Hallar el área bajo las gráficas de las funciones siguientes:

Evaluar las integrales:

Se aplica una fuerza f(x)=e^2x, en newtons, para mover una caja desde la posición x=2 hasta x=6 (en metros) sobre el piso. Evalúe el trabajo realizado.

Un resorte requiere una fuerza de 3 newtons para ser estirado un metro. Calcule el trabajo necesario para estirarlo 2 metros más.

La rapidez de cambio en la población de un cultivo de bacterias en el tiempo t (en horas) se modela por: P´(t) = e^2t. Si la población inicial se estima como P₀ = 10², determine la población P(t) a las 10 horas y el incremento de la población entre las 5 y las 10 horas.

tomado de: http://navarrof.orgfree.com/Docencia/MatematicasII/M2UT4/aplicaciones_integral.htm

Enseñanza del concepto de área

El concepto de área está tan vinculado a nuestras actividades cotidianas que tomar conciencia de él es tan difícil como percibir el aire que respiramos. Su origen es tan viejo como la humanidad, pero su formulación matemática precisa, lograda recién cuatro siglos atrás, es hoy sólo patrimonio de unos pocos profesionales de las ciencias exactas. Para terminar con esta indeseable situación hay que modificar la enseñanza del concepto de área desde la escuela primaria. El presente artículo propone una manera de hacerlo.

Introducción

• ¿Cuántos pliegos de cartulina debemos tener para poder hacer 25 sombreritos para la fiesta de cumpleaños?
• ¿Cuántos mosaicos hay que comprar para reemplazar el piso de la cocina?
• ¿Qué cantidad de tela se requiere para hacer un juego de sábanas para nuestra cama?
• ¿Cuántos litros bastan para dar 3 manos de pintura al salón de conferencias?
• ¿Cuanta semilla alcanza para replantar todo el césped del jardín?
• ¿Cuántos camiones necesitaremos para acarrear la tierra obtenida al sacar una capa de 10 cm de todo el patio?
• ¿Qué productividad tiene la tierra agraria de una zona?
• ¿Qué tamaño de departamento necesitamos para satisfacer bien nuestras necesidades familiares de espacio?
• ¿Qué extensión tiene la cuenca del río Paraná?

Para contestar cualquiera de estas preguntas, y muchas otras, necesitamos comprender y saber calcular áreas. Se trata, en todos los casos, de cuantificaciones de superficies en relación con otras magnitudes muy variadas.

Origen histórico del concepto de área

A diferencia de las leyes físicas, químicas y biológicas, los conceptos matemáticos no son parte de la naturaleza sino provienen de la interacción de la mente humana con ella. Reflejan la manera en que está estructurado el pensamiento, sus elementos constitutivos, las relaciones entre ellos y las operaciones de transformación de ambos (estructurasy procesos mentales). Durante el proceso de evolución biológica de la especie humana estas características se adaptaron a la mejor resolución de sus problemas prácticos. Es por esta razón que la valoración y el rescate de la intuición del estudiante —experiencia internalizada no consciente, véase el artículo sobre saber— le facilita asumir el protagonismo activo de su propio aprendizaje, en vez de ser un desganado memorista que sólo busca satisfacer los aparentemente arbitrarios requerimientos de un maestro o profesor. Ésto es justamente lo que pasa cuando el concepto de área se desarrolla a partir de la aparentemente antojadiza definición de la de un cuadrado o rectángulo.

El concepto de área no es innato sino culturalmente transmitido. Se originó probablemente en tiempos prehistóricos cuando la especie humana era todavía nómade y vivía de la caza, la pesca y la recolección de frutos y raíces. La búsqueda de alimentos requería grandes recorridos en busca de las plantas y animales esenciales para la supervivencia. Al mismo tiempo, la competencia con otros grupos humanos requería respetar territorios ajenos o combatir por ellos, siendo el concepto de territorio afín al de área. En esta acepción operativa un área es una franja de territorio que se puede recorrer en cierto tiempo, dependiendo de la naturaleza del terreno y de la velocidad de desplazamiento. Este mismo concepto de área es el que tiene hoy aplicación práctica en un scanner, dispositivo electrónico que explora las características gráficas de una superficie por desplazamiento sobre ella, cuya correcta denominación castellana debería ser explorador por barrido.

La segunda acepción operativa de área —más básica, la usada en las ingenierías y en la Física— es la de cubrimiento y requiere un área de referencia como una manta, una alfombra o una baldosa. Esta acepción seguramente surgió en la etapa sedentaria de los asentamientos humanos estables, de la construcción de viviendas permanentes y de la ocupación continua de terrenos agrícolas y ganaderos. No se puede calcular la cantidad de semilla necesaria para cubrir un terreno de cultivo ni fabricar la cantidad de tela necesaria para vestir a una persona si no se tiene alguna manera de medir o calcular áreas. En esta acepción dos superficies cualesquiera (la del cuerpo y la de la tela, en el segundo ejemplo) tienen la misma área cuando una es capaz de cubrir a la otra sin sobrantes ni faltantes apreciables. Esta acepción, más simple, puede servir de fundamento a la primera acepción discutida, la del recorrido, que puede entonces considerarse como un proceso de cubrimiento virtual

Áreas de figuras irregulares

El concepto de cubrimiento se cuantifica cuando se usa una superficie de referencia (unidad) capaz de cubrir, por repetición, otra mucho mayor. Aquí es crítica la forma de la unidad para que sea capaz de cubrir áreas crecientes, por repetición y sin dejar huecos entre sí. Hay muchas formas con esa propiedad, siendo las más conocidas —por su uso en baldosas y azulejos— los cuadrados (véase la Figura 1) y rectángulos. Otras menos comunes son el triángulo equilátero, como se ilustra en la Figura 2, los paralelogramos de cualquier forma y los exágonos regulares. Es imposible, en cambio, cubrir una superficie con pentágonos regulares sin dejar huecos entre ellos (véase la Figura 3). Es importante aquí establecer bien la diferencia entre la ausencia de huecos y solapamientos entre piezas contiguas y la capacidad de cubrir cualquier forma sin excesos ni sobrantes, tema que se discute detalladamente a continuación.

 

Figura 1. Cubrimiento de una superficie              Figura 2. También puede hacerse
               con cuadrados                                                        con triángulos equiláteros.

• 

  
  Figura 3. El cubrimiento con pentágonos regulares es siempre incompleto.
 
• 

  
  Figura 4. El área aproximada de la superficie, por defecto, es de 16 unidades y 17/4.

El grado de cubrimiento de figuras irregulares es mayor cuanto menor sea la unidad de área (el área de referencia). Para ello hay que subdivir esta área en fracciones, que en el caso de la Figura 4 son 1/4 de la unidad original para facilitar su visualización (la norma decimal es subdividir la unidad principal en décimas, centésimas, y así siguiendo). Si siguierámos subdividiendo aún más la unidad, lograríamos aproximarnos cada vez más a un cubrimiento completo, hasta el punto en que el error cometido fuera despreciable. El uso sucesivo de unidades cada vez más pequeñas hasta lograr el cubrimiento completo es la base del concepto matemático de área que se discute al final. El cubrimiento aproximado puede hacerse tanto por defecto (caso de la Figura 4) como por exceso (véase la Figura 8).

Elección de unidades de área

El cubrimiento permite determinar la igualdad de áreas, con un margen de error que depende de cual sea la menor fracción de la unidad de cubrimiento que se esté dispuesto a usar. En todo el análisis previo esta unidad era elegida arbitrariamente; podía ser una hoja de papel, un trozo de tela, una alfombra o cualquier otro objeto adaptable a la superficie cuya área se quiere determinar por comparación. Esta arbitrariedad —común a las unidades de cualquier magnitud, tales como una longitud, un tiempo o una luminosidad— crea problemas cuando se quiere comunicar áreas a alguien que no tiene acceso directo a la unidad. Por ejemplo, si alguien nos ofrece en EEUU un terreno cuya área es de 200 acres (unidad habitualmente usada en ese país), no sabremos de qué nos está hablando hasta que sepamos cómo compararla con nuestra unidad habitual para ese fin, la hectárea (ha).

La unidad adoptada universalmente por la Física (Sistema Internacional de unidades, o SI) es el área de un cuadrado de 1 metro de lado, o metro cuadrado (m², véase metro). Para grandes áreas la operación de cubrimiento se facilita si se toman múltiplos de la unidad principal. Nótese, por ejemplo, que la zona central de la Figura 4 puede cubrirse con una super-unidad cuadrada formada por 9 unidades principales. Cada unidad convencional tiene un rango práctico de aplicación: el cm² para superficies que caben en nuestras manos, el m² para departamentos, la hectárea (1 ha=10.000 m²) para lotes y el km² (100 ha) para las áreas de provincias y países.

Áreas de figuras regulares

Figura 5. Cálculo del área de un rectángulo por cubrimiento con unidades cuadradas.

Las figuras más simples que se pueden recubrir de modo perfecto son los rectángulos cuyos lados son múltiplos enteros del lado de la unidad cuadrada de área (múltiplo o submúltiplo del m²). El rectángulo de la Figura 5, cuyos lados miden respectivamente 3 y 5 unidades de longitud (los segmentos indicados), se puede cubrir completamente con cuadraditos cuyos lados miden 1 unidad de longitud, y cuyo número, como se ve a simple vista, es el producto de las medidas de los lados. Para mayor claridad del argumento estos rectángulos se representan separados a la derecha de la figura. Esta propiedad es completamente general y conduce a la fórmula del área de un rectángulo como el producto de su base por su altura. No es una definición inventada sino una consecuencia del concepto de área como medida del cubrimiento. La definición es válida también para lados que no son múltiplos enteros, sino cualquier fracción del lado del cuadrado unidad de área. Se puede verificar que esto es cierto usando como nueva unidad de área un cuadradito cuyo lado es también una fracción similar del original.

Figura 6. Cubrimiento de un rectángulo con dos triángulos de igual área.

Con este modo de introducir el concepto de área es fácil comparar el área de un triángulo con la de un rectángulo. En la Figura 6 se muestra la manera habitual de hacer esta reducción mediante la subdivisión de un triángulo escaleno, operación válida también para los triángulos equiláteros, isósceles y rectángulos (el caso más simple). Se traza la altura a del triángulo grisado, la línea de trazos, subdividiéndolo en dos triángulos rectángulos menores. Se construyen dos triángulos iguales a éstos, ubicándolos de modo de formar un rectángulo. Este rectángulo tiene un área doble que la del triángulo, porque para cubrirlo se requiere duplicar los triángulos originales. El área A del triángulo es, entonces, igual a la mitad de la del rectángulo así construido, la mitad del producto de su altura a por su base b: A=a·b/2.

Cuando el concepto de área se introduce, como es habitual, definiendo a la de un rectángulo como el producto de su altura por su base, el método gráfico de cálculo del área de un triángulo aparece como un artificio injustificado, cuando en realidad no es así. El problema surge porque se empieza con una fórmula, no con un concepto. Toda fórmula es la expresión matemática de un concepto cuya formación debe alcanzarse primero. El origen de este tradicional encaramiento probablemente proviene de que las definiciones operativas, como la de cubrimiento, son parte natural de la Física y las ingenierías, pero no de la Matemática. En ésta el método seguro no es el uso de la intuición sino la introducción de postulados, siendo la definición de área uno de ellos.

Todos los polígonos pueden reducirse a triángulos, por lo que su área se calcula por cubrimiento con triángulos apropiados, cuya área se conoce a partir de las medidas de sus bases (lados) y alturas (apotemas). Aunque aparentemente no puede calcularse de esta forma el área de un círculo, en realidad no es así. Este problema, que se encara a continuación, permitirá comprender mejor la idea de cubrimiento completo que se planteó al comienzo.

El área de un círculo y el concepto de límite

Figura 7. Cálculo del área del círculo por cubrimiento con sectores circulares.

Los matemáticos han desarrollado un método muy general para calcular el área encerrada por curvas cerradas expresables mediante funciones matemáticas. La más regular de todas estas curvas, en el sentido de que tiene la mayor cantidad de simetrías, es la circunferencia. El área de la superficie plana encerrada por una circunferencia (el círculo) se puede calcular cubriéndola con sectores circulares que pueden reordenarse para asemejarse a un rectángulo. Comenzamos, para aclarar ideas, con su cubrimiento con sólo 4 sectores circulares y luego dividimos cada uno de estos por 6 llevándolos a 24, como se muestra en la Figura 7. El cubrimiento es siempre perfecto cualquiera sea el número de sectores circulares usados, a diferencia de lo que sucedía en la Figura 4. La razón de aumentar su número es poder calcular su medida usando la fórmula básica del área del rectángulo. En efecto, cuanto más chicos sean los sectores circulares, más rectos se harán los bordes y más tenderá el “paralelogramo” a un rectángulo. Como se usa la mitad de los bordes externos de los sectores para formar el lado superior y la otra mitad para formar el inferior, su longitud es la misma e igual a la mitad del perímetro L de la circunferencia. Los lados “verticales” opuestos, por su parte, tienen longitudes iguales al radio R de la circunferencia. Por lo tanto, cuando los sectores circulares se hacen muy muy pequeños la figura tiende a un rectángulo cuya área vale A=R·L/2. La relación entre el perímetro L y el radio R de la circunferencia es L=2πRdonde π=3,14159... Reemplazando este valor de L en la fórmula del área se obtiene el conocido valor A=πR².

El proceso de cubrimiento recién descripto conduce al mismo resultado que la inscripción o circunscripción en la circunferencia de polígonos regulares con cantidad creciente de lados. El centro y los vértices del polígono determinan triángulos isósceles la longitud de cuya base se hace infinitesimal (tiende a cero). Este método general de calcular un área cualquiera usando elementos de cubrimiento cada vez menores, el llamado pasaje al límite infinitesimal, ya fue usado por los geómetras griegos hace más de 2.000 años. El uso de elementos de área infinitesimales es el punto de partida del cálculo integral inventado por Isaac Newton y Gottfried Leibniz hace casi 4 siglos, base imprescindible de la Física y las ingenierías actuales.

Figura 8. Octógono inscripto y circunscripto en una circunferencia.
El área gris corresponde al defecto y la negra al exceso de cubrimiento.

Del cubrimiento al concepto de integral

El cálculo de áreas mediante la operación matemática de integración se estudia en las escuelas industriales y universidades argentinas en las asignaturas Análisis Matemático. Una de las principales razones por las que los estudiantes tienen grandes dificultades para aprehenderlo en ambos niveles es porque su noción de área no incluye el cubrimiento.

Figura 9. Esta suma de infinitas áreas cada vez más pequeñas es finita.

En este método el número de áreas que se suman tiende a infinito y su tamaño tiende a cero. Es comprensible que para hacer un cubrimiento perfecto de superficies con bordes curvos, como la de la Figura 1, haya que usar subunidades cada vez más pequeñas. En cambio, es contrario a nuestra intuición que la suma de un número continuamente creciente de elementos pueda dar un resultado finito (véase Courant y Robbins, pp. 441‑446). Es por eso conveniente, antes de iniciar el tratamiento de las integrales, ejemplificar primero cómo puede suceder tal cosa. Se toma para ello un cuadrado de área A, se lo divide por la mitad para obtener un rectángulo de área A/2 y se lo adiciona al anterior. Luego se agrega la mitad de este rectángulo, un cuadrado de área A/4. Se prosigue de este modo con el proceso de subdivisión y agregado obteniendo alternadamente rectángulos y cuadrados cuyas áreas sucesivas son siempre la mitad de las precedentes. La Figura 9 ilustra cómo la suma de las áreas de las infinitas figuras así obtenidas, que son cada vez más pequeñas, da un resultado finito que en este caso es exactamente A. En efecto, el área no cubierta de la esquina superior derecha se reduce a la mitad en cada paso, tendiendo a 0 a medida que se siguen agregando figuras. En tan sólo 10 pasos el área sin cubrir es menor que un milésimo del área A. Esta secuencia corresponde a la denominada serie geométrica:

Figura 10. Definición de una integral.




Para definir con total precisión el área delimitada por una curva es necesario dar primero la descripción matemática de dicha curva a través del concepto de función y hacer su representación numérica en un sistema de coordenadas apropiado.

En el sistema de coordenadas cartesianas de la Figura 10 la curva superior está definida por la función y(x), cuyos valores para las abscisas indicadas son y_n=y(x_n). Las unidades elementales elegidas para cubrir el área comprendida entre la curva superiory el eje x son rectángulos de base constante Δ_x y altura variable y_n. Estos rectángulos tienen lados paralelos a los ejes coordenados x e y, y están asentados sobre el eje horizontal x. El área A₆ resultante del proceso de hacer tender a 0 el ancho de los rectángulos y a infinito su número, es la integral siguiente:

El símbolo ∫ representa la operación de suma. El símbolo dx, introducido por Leibniz, indica el pasaje de Δ_x al límite infinitesimal. El cálculo integral, aparentemente muy complicado, se vincula luego a un operación mucho más fácil de calcular, la derivación, tema que no se discutirá aquí ni las múltiples aplicaciones que el concepto tiene en muy variados campos del saber (véase, por ejemplo, Rey Pastor y otros, cap. XIII).

Figura 11. El área del círculo es A=A₁–A₂.

Pareciera que el método no es apropiado para evaluar áreas de superficies cerradas arbitrarias, pero no es así. Cuando la región cuya área se quiere calcular no contiene el origen del sistema de coordenadas cartesianas, hay que descomponer el borde de la región (la curva y(x)) en segmentos de modo tal que el área deseada pueda obtenerse por diferencia. Como la explicación escrita es más complicada que la visual, se remite al lector a la Figura 11 donde el área Adeseada se calcula como la diferencia de áreas A₁–A₂.

Figura 12. Cubrimiento con sectores circulares.

También es posible y frecuente el uso de elementos de área de forma muy variada (véase Granville), como los sectores circulares usados en las integrales polares que se muestran en la Figura 12 (Granville, pp. 629‑630). Estos sectores están determinados por su radio ρ_n, el ángulo polar θ_n que éste determina con el eje horizontal y su apertura Δ_θ, constante para todos ellos. Si la curva es una circunferencia y se elige el origen de coordenadas en su centro, el método se reduce al de la Figura 7. Este método es generalizable a sistemas de coordenadas muy variados que por regla general no se estudian en los cursos normales de Física e ingenierías (véase, desde el punto de vista de la Física, Stratton, pp. 47‑59).

Figura 13. Cubrimiento con cuadraditos infinitesimales.

Las integrales simples anteriores dan rigor matemático a un cubrimiento diferente del descripto en la Figura 4. El proceso allí esbozado tiene su realización matemática rigurosa recién cuando se introducen las integrales dobles que describen la suma de cuadraditos de lados Δ_x y Δ_y cuyas longitudes tienden a cero. La diferencia con el proceso descripto por la Figura 10 es que en este último caso no se usan cuadraditos sino rectángulos cuyo ancho Δ_x se hace tender a cero, pero cuya altura Δ_y es finita. Las integrales dobles que corresponden al proceso de subdivisión representado en la Figura 13 son (Granville, pp. 610‑613):

 

El tercero y cuarto miembro de esta ecuación describen cómo estas integrales dobles se reducen a una sucesión de dos integrales simples. Cuando la curva que delimita la superficie es suficientemente “regular” (concepto que requiere una especificación matemática compleja) esta reducción puede hacerse indistintamente en cualquiera de los dos órdenes indicados.

El cálculo de áreas mediante integrales dobles puede hacerse también en sistemas de coordenadas no cartesianas, como el de la Figura 12, pero este proceso no aporta conceptualmente nada nuevo.

Conclusiones

El concepto de área no surgió por caprichoso vuelo de la imaginación sino por las necesidades prácticas de cuantificar cubrimientos de muy variado tipo, entre los que podemos incluir algunos tridimensionales como los necesarias para la pintura de superficies no planas (caso de una cúpula). Ésto condujo naturalmente a la introducción de una unidad de superficie y de múltiplos y submúltiplos más apropiados para escalas mayores o menores que la original. La medida resultante (cantidad de unidades de referencia) es fácil de calcular cuando la unidad de cubrimiento es una forma regular simple como el rectángulo. Ésto no impide —de hecho es necesario en casos como el del círculo— el uso de unidades de cubrimiento de formas muy variadas cuya área, sin embargo, sigue cuantificándose en términos de cuadrados de tamaño apropiado (cm², m², ha = hm², km²...). Trabajar el concepto de área sólo para figuras regulares puede ayudar a desarrollar el concepto de medida, pero no basta para las aplicaciones prácticas que motivan la introducción del concepto. Es por ello necesario desarrollar la noción de cubrimiento desde el mismo comienzo de su estudio.

Cuando se tiene una superficie que no puede cubrirse de manera exacta con triángulos (la figura más pequeña para la que se tiene una fórmula simple), para obtener un cubrimiento (medida) perfecto es necesario recurrir a subunidades cada vez más pequeñas. La necesidad del pasaje al límite no es, por lo tanto, un artificio para la definición de integrales matemáticas sino un producto de la necesidad de hacer cubrimientos perfectos de superficies irregulares. Aunque desde el punto de vista práctico la precisión total no interesa, la Matemática la requiere de modo ineludible por razones que no es posible discutir aquí. Cuando se ilustra de modo apropiado, el concepto de pasaje al límite no es tan difícil como habitualmente se cree, aunque si lo es su definición matemática rigurosa (véase Klein, pp. 211‑220). Este concepto es imprescindible para el tratamiento matemático de cualquier tecnología compleja y debería ser trabajado, en etapas apropiadas, en las escuelas primarias (para las que el esbozo dado en la primera parte de este trabajo es suficiente) y secundarias (donde hay que desarrollar temas adicionales).

La construcción del concepto de área, desde su origen intuitivo en operaciones de cubrimiento hasta su rigurosa formulación matemática, requiere (como todos los saberes complejos) transitar un largo camino. La mente humana construye las estructuras complejas en etapas y niveles de agregación. La identificación de esas etapas, su jerarquización y la manera de construir estructuras mentales donde los conceptos más complejos están basados en la organización de otros más simples en estructuras de inclusión como las de las muñequitas rusas mamuschkas, son requisitos esenciales para el buen trabajo docente. Como para el recorrido de cualquier trayecto, no sólo hay que saber el punto de partida sino también el de llegada, aunque no todos lo completen arribando, como en este caso, al concepto de integral matemática.

Fuentes

• Courant, Richard & Robbins, Herbert; Qué es la Matemática; Editorial Alda; Ciudad de Buenos Aires; 1954; Courant&Robbins M.
• Granville, William Anthony; Cálculo diferencial e integral; Edit. UTEHA; México; 1956.
• Klein, Felix; Elementary Mathematics from an advanced standpoint: Arithmetic – Algebra – Analysis; Edit. Dover; New York (EEUU).
• Rey Pastor, J. y Pi Calleja, P. y Trejo, C. A.; Análisis Matemático, vol. 1; Editorial Kapelusz; Buenos Aires; 1952.
• Solivérez, Carlos E.; Del concepto intuitivo al concepto matemático de área. Versión inicial de este artículo.
• Stratton, Julius Adams; Electromagnetic theory; Edit. McGraw Hill; New York (EEUU); 1941.

tomado de:http://cyt-ar.com.ar/cyt-ar/index.php/Ense%C3%B1anza_del_concepto_de_%C3%A1rea