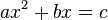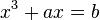CHISTE N° 61

Teorema: "Los científicos nunca ganan tanto dinero como los ejecutivos".

La siguiente demostración matemática explica este hecho.

Postulado 1: El Conocimiento es Poder (Energía).

Postulado 2: El Tiempo es Dinero.

Demostración.-

Como es sabido: Trabajo / Tiempo = Energía

Considerando que    Conocimiento = Energía   y   Tiempo = Dinero,

tenemos que:     Trabajo / Dinero = Conocimiento

Despejando Dinero, se obtiene:    Trabajo / Conocimiento = Dinero

Así que, cuando el Conocimiento tiende a cero, el Dinero tiende a infinito, independientemente del Trabajo realizado.

Conclusión: Cuanto menos sepas, más dinero ganarás...

TOMADO DE:http://catedu.es/matematicas_mundo/HUMOR/humor4_teoremas.htm

DESCOMPONER Y RECOMPONER EL PROBLEMA

BUSCAR UN PROBLEMA AUXILIAR 

Se trata de reducir el problema inicial a otro equivalente que sea más fácil de resolver.

            Ej: El cambio de variable en las ecuaciones bicuadradas cumple ese objetivo

Si tenemos       x⁴ - 13x² + 36 = 0

el cambio         x² = y

nos deja           y² - 13y + 36 = 0, ecuación de segundo grado

           Ej: La tipificación de una variable estadística X normal, N (m , s) para poder

           trabajar con otra variable  Z =(X - m ) / s   que sea  N (0 , 1), que está tabulada.

 DESCOMPONER Y RECOMPONER EL PROBLEMA

Si se trata de un "problema por resolver", una vez comprendido el problema como un todo, hay que entrar en detalles. Es aconsejable comenzar haciéndose las siguientes preguntas: ¿Cuál es la incógnita?, ¿cuáles son los datos?, ¿cuál es la condición?.

Después de descomponer el problema, tratamos de recomponer sus elementos de un modo diferente:        

           a) conservando la incógnita y cambiando los datos y la condición.

           b) conservando los datos y cambiando la incógnita y la condición.

           c) conservando la condición y cambiando la incógnita y los datos.

            Ej: los problemas "construir un triángulo equilátero, dado uno de sus lados" y

                 "construir un triángulo equiángulo, dado uno de sus lados"

                 corresponden a una transformación del tipo b).

Estas recomposiciones pueden proporcionarnos problemas intermedios que actúen como peldaños para la resolución de nuestro problema.

Si se trata de un "problema por demostrar", los cambios se realizan sobre la hipótesis o la conclusión.

ELIMINAR LOS TÉRMINOS TÉCNICOS

En ocasiones la esencia del problema nos queda encubierta por la terminología. Entonces,  hay que"regresar a las definiciones" para reformular el problema.

Ej: Determinar el punto de intersección de una recta dada y de una parábola cuyo foco y directriz son conocidos.

Si recordamos que la parábola es el lugar geométrico de los puntos equidistantes del foco y de la directriz, podremos reformular el problema así:

Determinar un punto P sobre una recta dada r, que esté a igual distancia de un punto y de una recta conocidos.

El nuevo enunciado carece de términos técnicos y nos centra en la esencia de la situación.

TOMADO DE:http://catedu.es/matematicas_mundo/PROBLEMAS/problemas_varios.htm

José María Sorando Muzás    jmsorando@ono.com 

FRANCOIS VIETE

En el Renacimiento hubo desarrollos trascendentes en álgebra. Sin embargo, merecen ser mencionadas algunas obras que contribuyeron a que esta rama de las matemáticas no quedase en el olvido.
Pero sin duda el cambio más significativo en el carácter del álgebra relacionado con el simbolismo fue introducido por François Viète (1540-1603) un abogado francés cuyo interés por las matemáticas era puro entretenimiento y describe su In Artem Analyticam Isagoge como la obra del análisis matemático restaurado. 
Viète traza la línea divisoria entre la aritmética y el álgebra y propone utilizar una vocal para representar una cantidad que se supone en álgebra desconocida o indeterminada, y una constante para representar una magnitud o un número que se supone conocido o dado. 
Esta distinción entre el concepto de parámetro y la idea de incógnita fue un paso previo a la matemática moderna.

François Viète
Fue un matemático francés (Fontenay-le-Comte, 1540-París, 1603). Se le considera uno de los principales precursores del álgebra. Fue el primero en representar los parámetros de una ecuación mediante letras.
François Viète también fue conocido en su época como súbdito del rey fiel y competente. Fue consejero privado de los reyes de Francia Enrique III y de Enrique IV.
Hijo de un procurador, Viète estudiaba derecho en Poitiers. En 1560, se convierte en abogado en Fontenay-le-Comte. Se le confían de golpe importantes asuntos, v

En 1571, pasa a ser abogado en el Parlamento de París, y se le nombra consejero en el Parlamento de Rennes en 1573. En 1576, entra al servicio del rey Enrique III, quien le encomienda una misión especial. En 1580, pasa al servicio exclusivo del rey en el Parlamento de París.
También en 1580 Viète se encarga de un importante pleito que opone al duque de Nemours con Françoise de Rohan, y que se falla en beneficio de esta última. Esto le valió el odio de la Liga Católica, que conseguirá en 1584 que se le aparte de sus funciones. Enrique de Navarra redactará varias cartas en favor de Viète, intentando que recuperara su puesto al servicio del rey, pero no se le escuchará. Viète dedica esos años en los que se verá apartado de la vida política a las matemáticas.
Expulsado de París en 1589, tras la jornada de las barricadas, el 12 de mayo de 1588,

Enrique III se ve obligado a refugiarse en Blois. Hace un llamamiento a los oficiales reales para que se reunan con él en Tours antes del 15 de abril de 1589: Viète responde a este llamamiento entre los primeros.
Tras la muerte de Enrique III, Viète pasa a formar parte del consejo privado de Enrique IV,quien lo admira mucho por su talento matemático. A partir de 1594, se encarga exclusivamente de descifrar los códigos secretos enemigos, tarea que venía desarrollando desde 1580.
En 1590, Enrique IV había hecho pública una carta del comendador Moreo al rey de España. El contenido de dicha carta, que Viète había descifrado, revelaba que el jefe de la Ligaen Francia, el duque de Mayenne, aspiraba a convertirse en rey en lugar de Enrique IV. Esta publicación puso en una situación delicada al duque de Mayenne y favoreció el desarrollo de las guerras de religión.
El memorándum que redactó en 1603, poco antes de morir, sobre cuestiones de criptografía dejó obsoletos los métodos de cifrado de su época.
Enfermo, dejó el servicio del rey en 1602 y muere en 1603.

Primeros Trabajos 
Durante el Renacimiento las actividades matemáticas lograron avances muy importantes en el campo del álgebra, la trigonometría y la geometría. Ya se utiliza un simbolismo rudimentario en álgebra, lo símbolos indo arábigos están suficientemente extendidos, las fracciones decimales se desarrollan poco a poco y la teoría de las ecuaciones ha logrado comprender la solución general de la cúbica y la bicuadrática. Los números negativos se aceptan progresivamente y la trigonometría, considerada ciencia independiente, dispone ya de tablas muy precisas para las seis funciones. En cuanto a la geometría, se desarrollan nuevas orientaciones en geometría descriptiva y proyectiva. Todos estos avances son ampliamente difundidos de forma más normalizada gracias a la imprenta.

La aplicación de todos estos conocimientos a campos tan diversos como la cartografía, el arte, la óptica o la contabilidad sirvió para relanzar las matemáticas y darles un impulso de modernidad, con un sentido más crítico de los modelos clásicos, intentando definir otros nuevos que los sustituyeran.
A esta etapa de la culminación del Renacimiento y comienzo de las matemáticas modernas contribuyó de forma especial François Viète.
En el periodo que va de 1564 a 1568 escribió dos obras, una de astronomía titulada Harmonicon coeleste que no llegó a publicarse y su gran Canon mathematicus seu ad triangula, cuya impresión duró más de ocho años y se publicó en 1579. Las aportaciones de esta obra fueron, entre otras, la utilización sistemática de los números decimales, con empleo de la coma; la aplicación sistemática del álgebra a la trigonometría descubriendo de nuevo la mayor parte de las identidades elementales con fórmulas generales para las expresiones de las funciones; la obtención de fórmulas trigonométricas de conversión del producto de funciones en una suma o una diferencia, o la obtención de lo que hoy se conoce como teorema del coseno.

En su obra Variorum de rebus mathematicis, de 1593, formuló un enunciado equivalente al teorema de la tangente.
Pero su fama le vendría por su contribución al álgebra, con su obra In artem analyticam isagoge, que se publicó por primera vez en Tours en 1591. Sirvió para la generalización del álgebra simbólica, muy parecida a la que después Descartes culminó. Viète utilizaba las vocales para identificar a las incógnitas y las consonantes para nombrar los parámetros conocidos (al contrario que ahora), pero aún utilizaba abreviaturas para identificar operaciones. 
Así, por ejemplo, para nombrar la ecuación 2ax² + 3bx - x³ = D hacía lo siguiente: la x la nombraba A; los parámetros a y b los nombraba B y F; al D lo llamaba solido; a la operación de multiplicar, in; el cuadrado, q (de quadratus); el cubo era c (de cubus), y la igualdad era aequatur. 
Escribía: 
B 2 in A q + F 3 in A - A c aequatur D solido
Tras su muerte, en 1615, se publicó su obra De aequationum recognitione et emendatione, con estudios precisos sobre las raíces de las ecuaciones polinómicas.
Con Viète alcanzó el álgebra un grado de generalización notable y dio nuevos enfoques a la resolución de todo tipo de ecuaciones.

La Logística Especiosa Los matemáticos del Renacimiento se sentían continuadores de las matemáticas griegas, que son fundamentalmente geometría. En la época de Viète el álgebra, derivada de la aritmética, se percibe sólo como un catálogo de reglas. Algunos matemáticos, entre los que se cuenta Cardan en 1545, utilizaban razonamientos geométricos para justificar métodos algebraicos.

Así, la geometría parecía ser un instrumento seguro y potente para resolver cuestiones algebraicas, pero la utilización del álgebra para resolver problemas geométricos parecía mucho más problemática. Y, sin embargo, ésa era la propuesta de Viète.
A partir de 1591, Viète, que era muy rico, empezó a publicar a sus expensas la exposición sistemática de su teoría matemática, a la que llama logística especiosa o arte del cálculo sobre símbolos.
La logística especiosa procede en tres tiempos:
En un primer tiempo, se anotan todas las magnitudes presentes, así como sus relaciones, utilizando un simbolismo adecuado que Viète había desarrollado. A continuación, se resume el problema en forma de ecuación. Viète llama a esta etapa la zetética. Escribe las magnitudes conocidas como consonantes (B, D, etc.) y las magnitudes desconocidas como vocales (A, E, etc.).
El análisis porístico permite a continuación transformar y discutir la ecuación. Se trata de encontrar una relación característica del problema, la porisma, a partir de la cual se pueda pasar a la siguiente etapa.
En la última etapa, el análisis rético, volvemos al problema inicial del que exponemos una solución por medio de una construcción geométrica basada en la porisma.

Entre los problemas que Viète aborda con este método, hay que citar la resolución completa de las ecuaciones: 

De segundo grado de forma: 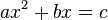  y de las ecuaciones de tercer grado de forma  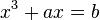con  y  positivos (Viète pone los cambios de variable sucesivos:  y  llevándolo de ese modo a una ecuación de segundo grado).

tomado de: http://www.buenastareas.com/ensayos/Francois-Viete/45244114.html

CHISTE N° 60

TOMADO DE:matematicasenelinstituto.blogspot.com

PARADOJAS

1. LA PARADOJA DEL MENTIROSO: Se atribuye a Epiménides haber afirmado: "Todos los cretenses son mentirosos". Sabiendo que él mismo era cretense, ¿decía Epiménides la verdad?

2. UN ENUNCIADO Y SU CONTRARIO: "Esta frase consta de siete palabras." Está claro que su enunciado es falso, ya que consta de seis. Por tanto, su contrario debería ser verdadero. ¿Es esto correcto?

3. LOS TRES ENUNCIADOS FALSOS: Tenemos aquí tres enunciados falsos. ¿Será capaz Ud. de descubrir cuáles?

1) 2+2=4

2) 3x6=17

3) 8/4=2

4) 13-6=5

5) 5+4=9

4. APROBARÁ EL EXAMEN: El siguiente relato ocurrió en un examen oral. PROFESOR: De las siete preguntas de que consta el examen, ya te has equivocado en tres preguntas, y sólo nos queda una. Tu aprobado o suspenso depende completamente de si aciertas o no la próxima pregunta. ¿Te das cuenta?

ALUMNO: Sí. Me doy cuenta.

PROFESOR: El estar nervioso no te ayudará.

ALUMNO: Ya lo sé. Trataré de tranquilizarme.

PROFESOR: Y esta es la pregunta. Recuerda: todo depende de si contestas esto bien o mal.

ALUMNO: Sí, sí, ¡ya lo sé!

PROFESOR: La pregunta es ésta: ¿Aprobarás este examen?

ALUMNO: ¿Cómo voy a saberlo?

PROFESOR: Eso no es una respuesta. Debes darme una respuesta clara, sí o no. Si contestas bien, aprobarás; si no, suspenderás. ¡Así de simple!
La cuestión no le parecía nada simple al alumno. La verdad es que cuanto más pensaba en ello más confuso se sentía. Y de repente cayó en la cuenta de algo muy interesante. Si contestaba una cosa, el profesor tendría la posibilidad de aprobarle o suspenderle, como más le complaciera. Si contestaba lo otro, sería imposible que el profesor le aprobara o le suspendiera sin contradecir sus propias reglas. Como el alumno tenía más interés en no suspender que en aprobar, eligió la segunda alternativa, y contestó de una manera que confundió por completo al profesor. ¿Qué respuesta dio?

5. UNA DE LAS DOS: He aquí dos afirmaciones. Una de ellas es falsa. ¿Cuál?

6. ERRORES: En éste se cometen tres errores.

París es la capital de Francia.

Dos más dos es igual a cinco.

América fue descubierta en 1.492.

¿Cuáles son los errores?

7. HORRORES: En éste se cometen dos errores.

Roma es la capital de Italia.

Dos por dos es igual a cinco.

Hillary escalé el Everest.

¿Cuáles son los errores?

8. PARADOJA MECÁNICA: ¿Por qué los camiones que transportan leche de vaca son una paradoja mecánica?

9. PARADOJA TEMPORAL: Un español en 1.987 llamó por teléfono a otro que se encontraba en 1.986, y le dijo:

- Mañana te telefonearé de nuevo.

- De acuerdo. ¡Hasta mañana!

¿Podría darse esta situación un tanto paradójica en la vida real?.

SOLUCIONES DE LAS PARADOJAS

1. LA PARADOJA DEL MENTIROSO.

2. UN ENUNCIADO Y SU CONTRARIO. ¡Es falso! La oración contraria: "Esta frase no consta de siete palabras." está formada exactamente por siete palabras. ¿Cómo resolver estos raros dilemas?

3. LOS TRES ENUNCIADOS FALSOS. Únicamente son falsos los enunciados 2 y 4. Por tanto, la afirmación de hay tres enunciados falsos es falsa. Tenemos así el tercero de los enunciados falsos. ¿No es verdad?

4. APROBARÁ EL EXAMEN. Supongamos que contestara que sí. En este caso el profesor podría suspenderla o aprobarle, como prefiriese. Si le suspendía y el alumno preguntaba por qué, el profesor podría decir "Contestaste mal la última pregunta, después de todo dijiste que ibas a aprobar y no fue así, y como la última pregunta estaba mal, tienes que suspender". Pero el profesor podría igualmente aprobarle y decir "Dijiste que aprobarías, y como ha sido así, tenías razón, así que contestaste bien la última pregunta, y por eso apruebas". Desde luego los dos razonamientos son circulares, pero ninguno de los dos es peor que el otro.

En cambio, si el alumno contestara que no, el profesor no podría ni suspenderla ni aprobarle. Si le aprobaba, el alumno habría contestado mal y habría suspendido. Si le suspendía, el alumno habría contestado bien y habría aprobado. Así que el profesor no podía ni aprobarle ni suspenderla.

Como el alumno tenía más interés en no suspender que en aprobar, contestó "No" y fastidió al profesor por completo.

5. UNA DE LAS DOS. La primera es cierta: hay dos afirmaciones, ella misma y la segunda. ¿Y la otra? Si fuese falsa, ella misma habría de decir que no hay ninguna falsa (al ser falsa) y si fuese verdadera, ¿dónde está la falsa? Por lo que nos introducimos en una clara contradicción.

6. ERRORES. Hay dos errores; uno es la frase que dice «Dos más dos es igual a cinco». El otro es: «En este acertijo se cometen tres errores».

7. HORRORES. Se trata de una paradoja. Si suponemos que el único error es «Dos por dos es igual a cinco», entonces la primera frase debe ser correcta; pero no puede serlo, porque afirma que los errores son dos. Y si suponemos que los errores son, efectivamente, dos, la primera frase debe estar equivocada; pero no puede estarlo, porque afirma precisamente que los errores son tantos como supusimos. Luego este acertijo no tiene solución lógica.

8. PARADOJA MECÁNICA. Porque cuánta más leche llevan, más despacio van.

9. PARADOJA TEMPORAL. Por paradójica que parezca es posible con la condición de que el primer español se encuentre en la Península y el otro en las Islas Canarias y que la llamada se realice en la Península después de las 12 de la noche del 31 de diciembre y antes de la una de la madrugada del día 1 de enero.

TOMADO DE:http://analisisfigempa.wikispaces.com/paradojas+o+acertijos+matem%C3%A1ticos

PROBLEMAS SOLUCIONADOS DE RAZONAMIENTO

Los sombreros

En un manicomio sobra gente y el director decide hacer un examen a los enfermos para determinar cuál es el más inteligente y darle la libertad. Hay tres enfermos que realizan el examen con total perfección y el director decide hacerles otra prueba. Los reúne en una habitación carente de superficies reflectantes y les dice: "Aquí tengo cinco sombreros: dos negros y tres blancos. Apagaré la luz y os pondré uno a cada uno. Luego la encenderé y sólo podréis ver los sombreros de los demás. Empezaré a preguntar uno por uno de qué color lleva el sombrero y aquél que lo adivine y sea capaz de razonar su respuesta será libre". Y así se hizo. Cuando el director pregunta al primer enfermo, éste no es capaz de adivinar el color de su sombrero con la información de que dispone. El segundo tampoco fue capaz. Pero ¿qué dirá el tercero?

una solución

Pensemos qué ocurriría si el sombrero del tercer "concursante" fuese negro. En ese caso el primer "loco" sería incapaz de adivinar el color de su sombrero sólo si el sombrero del segundo fuese blanco. Pero este razonamiento puede hacerlo el segundo participante (que también ve el sombrero del tercero) y concluir con ello que su sombrero es blanco. Sin embargo, el segundo concursante no fue tampoco capaz de adivinar el color de su sombrero, por tanto el sombrero del tercero no puede ser negro: ha de ser blanco.
Sin embargo, para ser rigurosos, no hemos demostrado si el problema tiene solución, sólo hemos demostrado que la solución no puede ser "negro". Supongamos que el sombrero del tercero es blanco y comprobemos si existe alguna situación en la que ninguno de los primeros concursantes sean capaces de adivinar el color de sus sombreros. Encontramos cuatro situaciones, de hecho la única condición para que ocurra lo que describe el enunciado es que el sombrero del tercero sea blanco. Tengamos en cuenta que el único caso en el que alguno de los participantes puede adivinar el color de su sombrero sin más información que el color de los demás sombreros es cuando esos otros dos sombreros son negros. Veamos las cuatro situaciones detalladamente:

• N N B: El primero no puede adivinar el color de su sombrero porque ve N B. El segundo comprende la incapacidad del primero porque ve un sombrero blanco pero no puede saber si su sombrero es blanco o negro porque sólo ve un sombrero negro.
• N B B: Este caso es similar al anterior, el razonamiento es el mismo.
• B N B: El primero no puede adivinar el color de su sombrero porque ve N B. El segundo comprende la incapacidad del primero porque ve dos sombrero blancos y no puede saber si su sombrero es blanco o negro porque existe un tercer sombrero blanco.
• El razonamiento es similar al del caso anterior.

Con todo esto, podemos afirmar que el razonamiento del primer párrafo es correcto y el sombrero del tercer personaje es blanco.

El club de golf

Un periodista va a un club de golf para escribir un artículo. Le habían dicho que en aquel club sólo había dos tipos de socios: los que siempre mienten y los que siempre dicen la verdad. Una vez acabada su ronda por el club le invitaron a asistir a una junta en la que estarían todos los socios. Éstos se encontraban sentados en una mesa redonda. Cuando acabó la junta el director le invitó a hacer una pregunta a cada socio y el periodista hizo a cada uno de ellos la misma pregunta: "¿Miente el socio que tiene a su derecha?". Curiosamente la respuesta de todos los socios fue la misma: "Sí". Una vez en su casa, el periodista se da cuenta de que se olvidó preguntar el número de socios del club, así que llama al secretario y este le dice: "Somos 51". Pero, de repente, se da cuenta de que el secretario puede mentir, así que llama al director quien le dice: "El secretario es un mentiroso. Somos 52". ¿Cuántos eran realmente? 

una solución

El primer detalle importante del enunciado que nos dirige a la solución es el hecho de que todos los socios respondan "sí" a la pregunta que el periodista les hace. Esto indica que el número de socios es par, veamos por qué. Cuando un socio admite que el de su derecha miente es porque: él es un mentiroso y el de su derecha dice la verdad o bien él dice la verdad y el de su derecha miente. En cualquier caso hay un mentiroso y un sincero juntos. Como esto ocurre con todos los socios, resulta que en la mesa están sentados de forma alternativa los mentirosos y los sinceros. Además el número de socios debe ser par, puesto que si no lo fuera tendría que haber dos socios con la misma "cualidad" juntos. Por tanto, está claro que el secretario miente y que el director dice la verdad. Sin embargo, hay que tener en cuenta que concluimos la veracidad del enunciado del director no porque haya dicho un número par (si fuera mentiroso, podría decir un número par que no fuera el correcto), sino porque ha dicho que el secretario miente, lo cual sabemos que es cierto. Por tanto, el número de socios es 52.

El tren

El tren de Rocío sale a las diez en punto. Si va a la estación caminando, a una velocidad de 4 Km/h, llega cinco minutos tarde. Si va corriendo, a 8 Km/h, llega con diez minutos de adelanto. ¿A qué distancia está Rocío de la estación?

una solución

Una primera solución a este problema podría ser expresar las ecuaciones que relacionan la velocidad con el tiempo y la distancia y resolverlas. Sin embargo, vamos aquí a razonar sin escribir las expresiones explícitamente. Lo primero que debemos observar es que cuando Rocío va hacia la estación a 4 Km/h tarda 15 minutos más que cuando va a 8 Km/h. Por otro lado, cuando Rocío corre lo hace al doble de velocidad que cuando va andando, por tanto debe tardar la mitad de tiempo. De todo esto deducimos que 15 minutos es la mitad de lo que tarda cuando va andando a 4 Km/h. Por tanto, andando tarda 30 minutos en llegar a la estación y una simple multiplicación nos desvela que ésta se encuentra a 2 Km.

TOMADO DE: http://neo.lcc.uma.es/staff/francis/spanish/acertijos.html

Cálculo Vectorial2

Cálculo Vectorial1

CHISTE N° 59

TOMADO DE:www.taringa.net

PROBLEMAS RESUELTOS DE LOGARITMOS

TOMADO DE:http://docencia.udea.edu.co/ingenieria/calculo/pdf/1_3_4.pdf

PROBLEMAS APLICATIVOS DE DERIVADAS

TOMADO DE:http://docencia.udea.edu.co/ingenieria/calculo/pdf/4_2.pdf

PROBLEMA DE RAZONES TRIGONOMÉTRICAS

Calcular:



si:
Cos (α +30º) × Sec (2α + 15º) = 1
Tg (3θ + 21º) × Tg (39º – θ) = 1

SOLUCIÓN:



TOMADO DE:http://www.problemasresueltos.com/matematica-preuniversitaria/trigonometria/razones-trigonometricas-de-angulos-agudos/529-razones-trigonometricas-de-un-angulo-agudo-solucion-2.html

PROBLEMARIO DE GEOMETRÍA ANALÍTICA

TOMADO DE:https://academica.ues.edu.sv/uiu/elementos_estudio/matematica/Jesus%20Infante%20Murillo%20-%20Geometria%20Analitica/12.%20Problemario.pdf

ECUACIÓN GENERAL DE SEGUNDO GRADO

TOMADO DE:https://academica.ues.edu.sv/uiu/elementos_estudio/matematica/Jesus%20Infante%20Murillo%20-%20Geometria%20Analitica/8.%20Ecuacion%20General%20de%20Segundo%20Grado.pdf

LA PARÁBOLA

TOMADO DE:https://academica.ues.edu.sv/uiu/elementos_estudio/matematica/Jesus%20Infante%20Murillo%20-%20Geometria%20Analitica/5.%20Parabola.pdf

Angulos y distancias

Distancia entre dos puntos

d=(x2−x1)2+(y2−y1)2+(z2−z1)2−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√

Vector normal a un plano

Primero calculamos la ecuación del plano que pasa por un punto A y es perpendicular a un vector n tal como se muestra en la figura. El vector u va del punto P(x,y,z) y el punto A(x₀,y₀,z₀)

El producto escalar de los vectores n y u deberá ser cero.

u=(x-x₀)i+(y-y₀)j+(z-z₀)k

n=ai+bj+ck

u·n=a(x-x₀)+b(y-y₀)+c(z-z₀)=0

ax+by+cz=d

que es la ecuación del plano. Las componentes del vector n normal al plano son los coeficientes a, b, c de x, y y zen la ecuación del plano. El vector unitario normal al plano es

nˆ=aa2+b2+c2−−−−−−−−−−√iˆ+ba2+b2+c2−−−−−−−−−−√jˆ+ca2+b2+c2−−−−−−−−−−√kˆ

Angulo entre dos planos

El producto escalar nos permite determinar el ángulo entre dos vectores u y v.

u⋅v=u⋅v⋅cosθu⋅v=uxvx+uyvy+uzvzcosθ=u⋅vu⋅v

Si n₁ y n₂ son los vectores perpendiculares a cada uno de los dos planos, el ángulo θ entre estos dos vectores es el mismo que el ángulo entre los dos planos. El ángulo entre los dos planos se calcula mediante la siguiente fórmula

a1x+b1y+c1z=d1 n1=a1iˆ+b1jˆ+c1kˆa2x+b2y+c2z=d2 n2=a2iˆ+b2jˆ+c2kˆcosθ=∣∣∣n1⋅n2n1⋅n2∣∣∣