MATEMÁTICA RECREATIVA

APLICACIONES DE LA TRIGONOMETRÍA

CURIOSIDAD MATEMÀTICA

El matemático ignorante 
En las aulas de cierta facultad de Matemáticas, nos podemos encontrar a un extraño personaje. Cierto día, me confesó que tan sólo sabía multiplicar y dividir por 2.
- A pesar de todo, me dijo, puedo multiplicar rápidamente números de dos cifras.
Le propuse que multiplicara 75 por 38.
Tomó una hoja de papel y escribió a la izquierda 75 y a la derecha 38. Luego inició sus cálculos:
- La mitad de 75 es 37, ¿no es así?.
- No -le dije- es 37'5.
- De acuerdo, pero no sé trabajar con decimales, así que no los pongo.
Escribió 37 y, repitiendo el proceso, dividió por dos y obtuvo, a pesar de mis protestas, 18, 9, 4, 2 y finalmente 1.
Después multiplicó 38 por dos. El resultado, 76, lo escribió en la fila inferior. Volvió a multiplicar por dos y obtuvo 152, 304, 608, 1216 y 2432.
Al final tenía escrito,

75	38
37	76
18	152
9	304
4	608
2	1216
1	2432

 
Me dijo que los números pares de la columna de la izquierda no servían de nada, así que los tachó (junto con el número que tenían a su derecha) con lo que quedó
 

75	38
37	76
9	304
1	2432

 
Sumando los números de la columna de la derecha obtuvo: 38+76+304+2432=2850, que es el resultado correcto. Probé con otros números y también funcionaba el método.
¿Sabrías dar una explicación matemática?.
TOMADO DE: http://rt000z8y.eresmas.net/matemat.htm#act10
Pagina creada por Ignacio A. Langarita Felipe

PROBLEMA DEL aceite y el vinagre

Un astuto especulador se inicia en los negocios con un lote de barriles de aceite y vinagre. No sabemos cuantos barriles hay de cada uno pero sabemos que su primer cliente pagó $14 por cierta cantidad de galones de aceite y $14 por cierta cantidad de galones de vinagre y que pagó el doble por el galón de aceite que por el de vinagre, finalmente le dejó un solo barril.

¿qué barril deja?

Solución

El cliente compró los barriles de aceite de 13 y 15 galones a 50 centavos por galón, y los barriles de vinagre de 31, 17 y 8 galones a veinticinco centavos por galón. Esto deja al barril de 19 galones, que puede contener tanto aceite como vinagre. 


See more at: http://www.puzzleclopedia.com/el-aceite-y-el-vinagre/#sthash.aYZMjwen.dpuf

PROBLEMA INTERESANTE

¿Qué pasaría si...

... cortáramos un cubo con un plano? ¿Podríamos obtener un triángulo semejante a cualquier triángulo dado?

SOLUCIÒN

Recordemos en primer lugar que dos triángulos son semejantes si los cocientes de los lados correspondientes son todos iguales a un número fijo. Por ejemplo, la Figura 1 muestra dos triángulos semejantes:

Figura 1.

Estos dos triángulos satisfacen las relaciones

Una vez hecha esta aclaración, la respuesta a la pregunta es que no es posible obtener un triángulo semejante a cualquier triángulo dado. Por ejemplo, veamos que este proceso de cortar el cubo con un plano no nos puede dar un triángulo recto. En la Figura 2 se ve un posible corte.

Figura 2.

Los tres triángulos que aparecen en otras tantas caras del cubo son rectos, por lo cual sabemos que se cumplen las siguientes relaciones:

Si además queremos que se cumpla, digamos, la relación , usando las tres relaciones anteriores podemos escribir:

de donde resulta , lo cual está claro que no puede ser. Desde luego, llegaríamos a una contradicción semejante si supusiéramos que el lado    ó el   es la hipotenusa del triángulo.

En este tema de cortar un cubo con un plano se pueden hacer muchas otras preguntas. Por ejemplo, ¿es posible obtener triángulos isósceles o equiláteros?, ¿es posible obtener un cuadrado o un rectángulo?, ¿se puede tener una sección pentagonal o hexagonal?, ¿qué polígonos regulares se pueden obtener?

Una manera divertida de experimentar es cortando patatas en forma de cubos y luego cortando los cubos de diferentes maneras. Los cortes, sumergidos en pintura, se convierten en sellos que pueden forman efectos interesantes sobre una hoja de papel.

	Sobre la autora
	Josefina (Lolina) Álvarez es Professor of Mathematics en New Mexico State University (USA). Especialista en análisis armónico y funcional, se doctoró en Matemáticas por la Universidad de Buenos Aires (Argentina), bajo la dirección de A.P. Calderón TOMADO DE: http://www.matematicalia.net/index.php?option=com_content&task=view&id=452&Itemid=275

MÈTODO DEL CANGREJO

Metodo cangrejo from Reynaldo Humberto Vera Yampi

CUATRO PREGUNTAS DE MATEMÁTICAS

1. ¿Cómo cortar el queso?   Los aficionados al queso de Camembert saben que este suele presentarse en piezas discoidales. Saben también que suele cortarse en sectores para su consumo, y que al dejar parte del queso cortado y sin consumir,la zona del del corte se seca y pierde su delicioso sabor. Procede pues, si no vamos a terminar en un día todo el disco de queso, cortarlo de la forma más eficaz posible para evitar pérdidas. Centraremos nuestra atención en el caso de que deseemos hace porciones del mismo tamaño. El problema, matemáticamente, se planteará así: Dado un círculo de radio unidad, ¿cómo dividirlo en n partes de la misma área de forma que el perímetro fronterizo sea de la menor longitud posible?
2. ¿Discriminación?Una empresa es acusada por un sindicato de discriminación sexual por contratar mayor proporción de hombres que de mujeres. La empresa alega que el promedio de contratación de mujeres en cada departamento es siempre mayor que el de hombres. Las afirmaciones de la empresa y del sindicato parecen contradictorias, pero, ¿podría suceder que ninguno mintiera?
3. Otra de naipes.Tomamos una baraja, volvemos la primera carta, la siguiente la colocamos debajo del mazo, volvemos la siguiente carta, la siguiente la volvemos a poner debajo y seguimos así hasta que estén todas vueltas. Resulta que las cartas han salido en orden creciente, primero oros, luego copas, luego espadas y finalmente bastos. ¿Cómo estaban colocadas en un principio?
4. Uno de cinemática.Dados dos puntos A y B situados en un plano vertical, encontrar otro punto C del mismo plano tal que dos móviles que parten de A y B simultáneamente cayendo por planos inclinados AC y BC se encuentren en C en un tiempo mínimo

SOLUCIONES:

1. Para n=2 ó n=3 las soluciones con triviales: el corte se hará según un diámetro en el primer caso, y según tres sectores de 120 grados en el segundo. 

Pero para n=4 la cosa comienza ya a complicarse. Pues un corte según cuatro sectores de noventa grados arrojaría una longitud de corte L=4, mientras que en el sistema indicado en la figura de la izquierda basta con L=3,9624. 

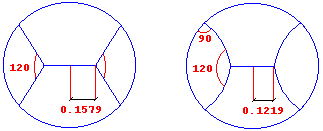
Esta división se ha obtenido recordando la conocida propiedad de que el punto situado en el interior de un triángulo cuya suma de distancias a los tres vértices es mínima es el que ve estos bajo ángulos de 120 grados. Sin embargo, todavía puede mejorarse: intuitivamente se comprende que, al no ser los segmentos rectos incidentes sobre la circunferencia perpendiculares a ésta podrían ser sustituídos por arcos de circunferencia que cumplieran con esta condición. Se mejora todavía algo, llegando a la figura de la derecha donde L=3,9412.

2.  Ambas entidades pueden tener razón porque más importantes que los promedios en sí mismos son las cantidades que dieron origen a esos promedios. Para ilustrarlo, lo mejor un ejemplo. En el departamento A se contrataron 4 de las 8 mujeres presentadas y 32 de los 80 hombres presentados. En el departamento B se contrataron 10 de las 40 mujeres presentadas y 4 de los 20 hombres. 

Estos datos conducen a un 50% y un 40% de contratación para mujeres y hombres en el departamento A, y un 25% y un 20% respectivamente, para el departamento B. En conjunto, la empresa ha contratado a 14 de las 48 mujeres (29,1%) y a 36 de los 100 hombres con lo que vemos que ambas afirmaciones eran ciertas.

3. Para explicarlo voy a suponer que sólo tengo las 10 cartas de un palo. La solución es fácilmente generalizable a cualquier número de cartas. 

Pensemos en que tenemos diez lugares en los que debemos ir colocando la carta adecuada. Es evidente que que los lugares primero, tercero, quinto, séptimo y noveno deberán estar ocupados por el As, 2, 3, 4 y 5. Una vez colocada la primera carta, el proceso que se ha seguido consiste en dejar un hueco y colocar la siguiente carta. Este es el proceso que deberemos aplicar hasta el final, pasar por alto un hueco y colocar la carta en el hueco siguiente. Por hueco entiendo cada uno de los lugares iniciales que aún están libres. 

Una vez colocado el 5 en el noveno lugar dejamos pasar el hueco décimo y ponemos el 6 en el siguiente hueco que es el segundo. Dejamos pasar el cuarto y colocamos el 7 en el sexto. Saltamos el octavo y ponemos la sota en el décimo y finalmente ponemos en rey en el cuarto. 

Las cartas de arriba a abajo, quedarían colocadas del siguiente modo: As, 6, 2, Rey, 3, 7, 4, Caballo, 5, Sota. 
Este procedimiento es extrapolable a cualquier número de cartas y generalizable para cualquier relación cartas vueltas/ cartas puestas.

4.  Para este problema se han recibido soluciones basadas en álgebra, pero resultan algo largas. Puede ser una buena ocasión para recordar el teorema de las esferas isocronas, tan útil en casos como éste, y que parece algo olvidado. Como es fácil comprobar, un móvil partiendo mediante un plano inclinado del polo N de una esfera alcanza cualquier punto de ésta en el mismo tiempo t = 2(R/g)½. 

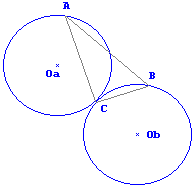
En el caso precedente, las dos esferas centradas en Oa y Ob deberán tener el mismo radio. La condición de tiempo mínimo exige que sean tangentes, así que dicho radio será la mitad de la distancia AB, igual, por paralelismo, a la OaOb. 

 

TOMADO DE: 

http://www.mensa.es/juegosmensa/e031035.html

http://www.mensa.es/juegosmensa/s031035.html#SOLU031