“Permíteme, querido amigo, volver un instante sobre la conversación que hemos tenido últimamente sobre el bello teorema de Jacobi relativo al número de descomposiciones de un entero en cuatro cuadrados, teorema que el iluste geómetra ha deducido primero de sus series elípticas y del que ha dado después una demostración aritmética….”
Así comienza el extracto de la carta de Lejeune-Dirichlet a Liouville, que éste publicó en su Journal de Mathematiques en 1856, y donde Dirichlet presenta una involución del conjunto de soluciones de 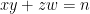 , para un
, para un  par dado, con
par dado, con 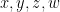 impares positivos y
impares positivos y  .
.
 Representamos una solución
Representamos una solución
Como 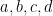 son impares,
son impares,  y
y 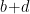 serán pares.
serán pares.
 Transformamos una solución reflejando primero su figura sobre una recta vertical y dividiéndola en tantas partes de anchura
Transformamos una solución reflejando primero su figura sobre una recta vertical y dividiéndola en tantas partes de anchura Separamos las partes, todas de anchura
Uniendo las partes una vez giradas tendremos la figura

que representa otra solución

Es claro, por el procedimiento de transformación de  en
en  que
que
son impares positivos y
.
y
.
- Aplicando la misma transformación a la solución
volvemos a obtener la solución original
.
Entonces la transformación que acabamos de describir es una involución del conjunto de soluciones impares positivas  de
de 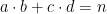 , con
, con 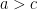 , que intercambia los valores de
, que intercambia los valores de  y
y 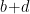 .
.
Soluciones impares, con a>c,
de a·b+c·d =
a x b + c x d a-c b+d
de a·b+c·d =
a x b + c x d a-c b+d
3 x 1 + 1 x 21 2 22
5 x 1 + 1 x 19 4 20
7 x 1 + 1 x 17 6 18
3 x 3 + 1 x 15 2 18
9 x 1 + 1 x 15 8 16
9 x 1 + 3 x 5 6 6
9 x 1 + 5 x 3 4 4
11 x 1 + 1 x 13 10 14
13 x 1 + 1 x 11 12 12
13 x 1 + 11 x 1 2 2
3 x 5 + 1 x 9 2 14
5 x 3 + 1 x 9 4 12
5 x 3 + 3 x 3 2 6
15 x 1 + 1 x 9 14 10
15 x 1 + 3 x 3 12 4
15 x 1 + 9 x 1 6 2
17 x 1 + 1 x 7 16 8
17 x 1 + 7 x 1 10 2
19 x 1 + 1 x 5 18 6
19 x 1 + 5 x 1 14 2
3 x 7 + 1 x 3 2 10
7 x 3 + 1 x 3 6 6
7 x 3 + 3 x 1 4 4
21 x 1 + 1 x 3 20 4
21 x 1 + 3 x 1 18 2
23 x 1 + 1 x 1 22 2
5 x 1 + 1 x 19 4 20
7 x 1 + 1 x 17 6 18
3 x 3 + 1 x 15 2 18
9 x 1 + 1 x 15 8 16
9 x 1 + 3 x 5 6 6
9 x 1 + 5 x 3 4 4
11 x 1 + 1 x 13 10 14
13 x 1 + 1 x 11 12 12
13 x 1 + 11 x 1 2 2
3 x 5 + 1 x 9 2 14
5 x 3 + 1 x 9 4 12
5 x 3 + 3 x 3 2 6
15 x 1 + 1 x 9 14 10
15 x 1 + 3 x 3 12 4
15 x 1 + 9 x 1 6 2
17 x 1 + 1 x 7 16 8
17 x 1 + 7 x 1 10 2
19 x 1 + 1 x 5 18 6
19 x 1 + 5 x 1 14 2
3 x 7 + 1 x 3 2 10
7 x 3 + 1 x 3 6 6
7 x 3 + 3 x 1 4 4
21 x 1 + 1 x 3 20 4
21 x 1 + 3 x 1 18 2
23 x 1 + 1 x 1 22 2
Para un  par dado, que se puede modificar, en el recuadro aparecen todas las soluciones
par dado, que se puede modificar, en el recuadro aparecen todas las soluciones  , con
, con 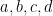 impares positivos y
impares positivos y  de la ecuación
de la ecuación 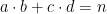 , y dos columnas adicionales con los valores de
, y dos columnas adicionales con los valores de  y
y 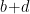 .
.
Por la involución descrita las columnas  y
y 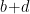 contienen los mismos valores con las mismas repeticiones, y para cada par
contienen los mismos valores con las mismas repeticiones, y para cada par 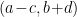 de la misma fila existe una fila en que aparece ese par invertido.
de la misma fila existe una fila en que aparece ese par invertido.
Si  no es múltiplo de 4, uno de los dos valores pares
no es múltiplo de 4, uno de los dos valores pares  ,
, 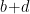 es múltiplo de 4 y el otro no lo es. Porque si
es múltiplo de 4 y el otro no lo es. Porque si  ,
, 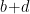 son los dos múltiplos de 4,
son los dos múltiplos de 4,  y
y 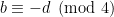 , y
, y  sería múltiplo de 4. Si ninguno de esos valores es múltiplo de 4, en los pares
sería múltiplo de 4. Si ninguno de esos valores es múltiplo de 4, en los pares  uno de los términos es de la forma
uno de los términos es de la forma  y el otro de la forma
y el otro de la forma  , y entonces
, y entonces 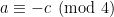 y
y , y
, y  sería múltiplo de 4.
sería múltiplo de 4.
De donde se concluye que si  no es múltiplo de 4, en la columna
no es múltiplo de 4, en la columna  (o
(o 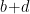 ) el número de elementos que son múltiplos de 4 es igual al número de elementos que no lo son.
) el número de elementos que son múltiplos de 4 es igual al número de elementos que no lo son.
En la siguiente entrada usamos este resultado para obtener, siguiendo a Dirichlet, el número de soluciones impares de la ecuación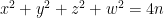 , para un
, para un  impar dado.
impar dado.
En la siguiente entrada usamos este resultado para obtener, siguiendo a Dirichlet, el número de soluciones impares de la ecuación
TOMADO DE:http://apolonio.es/guirnalda/una-involucion-de-dirichlet/#more-2730

No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.