Relación entre el cálculo integral y el cálculo diferencial.

Relación entre el cálculo integral y el cálculo diferencial.

Por: Miguel Solís Esquinca

Profesor de tiempo completo

Universidad Autónoma de Chiapas

En esta sección presentamos la relación que guardan la función derivada y la integral, convirtiendo a la integral en la operación inversa de la derivada. Hasta ahora, hemos considerado al área bajo una curva como un significado de la integral, expresado simbólicamente como

 = “área bajo la curva  desde a hasta b” (Figura 4.1)

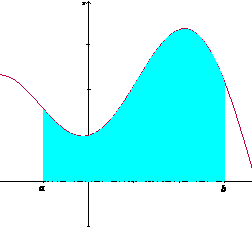
Figura 4.1

¿Qué sucede cuando uno de los límites de integración no es una constante sino una variable? Tendríamos que el área en cuestión sería también variable y dependería del valor de este límite variable de integración.

Imaginemos que queremos calcular el área bajo la curva 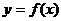 desde 0 hasta x (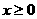). El área dependería de los valores que tomara x, esto es, el área sería una función de la variable x y podríamos expresarla como A(x) (Figura 4.2).

A(x)

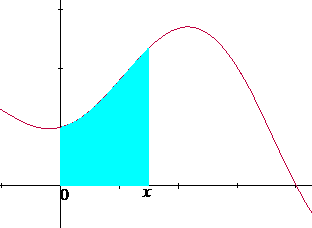
Figura 4.2

A(x) describe los valores del área bajo la curva f(x) en distintos momentos. Por ejemplo, A(x₁) y A(x₂) se puede considerar que representan dos valores del área en distintos momentos para los cuales A(x₁) sucedió antes que A(x₂) (Figura 4.3).

        

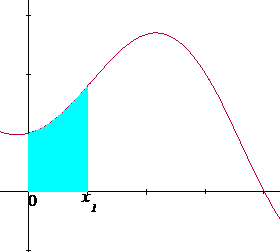
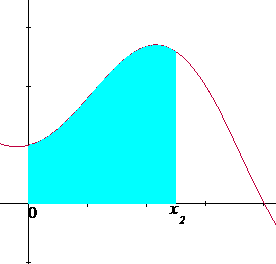
Figura 4.3

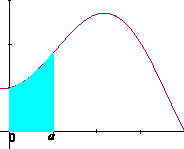
Utilizando esta idea de “área variable”, regresemos a la situación de calcular el área bajo la curva desde a hasta b, esto es: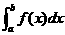. Pensemos que a y b son dos de estos momentos para los cuales el área toma los valores A(a) y A(b) y donde A(a) sucede antes que A(b), digamos que A(a) representa el valor inicial del área y A(b) el valor final. Para calcular el valor del área bajo la curva desde a hasta b debemos considerar el valor inicial y el valor final del área y efectuar la resta A(b) - A(a) (Figura 4.4).

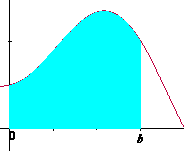
A(b)

A(a)

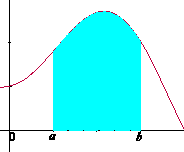
A(b) – A(a)

Figura 4.4

La resta A(b) - A(a) expresa el área acumulada entre a y b, en ese sentido la integral debe cumplir con la siguiente relación

Pero, ¿qué relación guardan las funciones A(x) (función área) y f(x)?

A(x), como lo dijimos anteriormente, describe valores del área bajo la curva f(x) en distintos momentos. La variación de estos valores es expresada por la diferencia

A(x+h)-A(x).

Geométricamente, la diferencia de áreas, resulta ser aproximadamente el área de un rectángulo de base h y altura f(x).

En la Figura 4.5 presentamos una secuencia gráfica considerando, primero el momento del área A(x), después el momento del área A(x+h), inmediatamente la resta de ambas áreas y, finalmente, la identificación del rectángulo de base h y altura f(x).

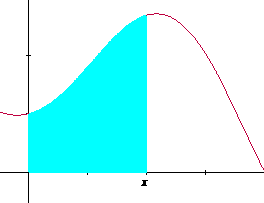
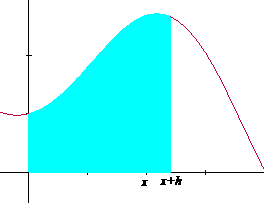
A(x)	A(x+h)
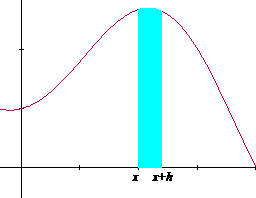
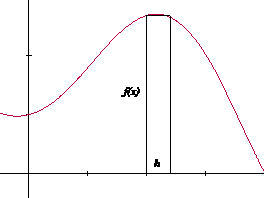
A(x+h) – A(x)	Rectángulo f(x)h

Figura 4.5

El área del rectángulo f(x)h es aproximadamente la variación o incremento del área A(x). Entonces,

donde 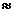 se lee “es aproximadamente igual a”

La razón de cambio del área se obtiene al dividir la variación entre h

y considerando el límite cuando h tiende a cero ()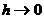

El lado izquierdo de la igualdad anterior es el límite de un cociente y no es mas que la definición de la derivada de la función A(x). De acuerdo a la geometría del área bajo la curva, hemos encontrado que la relación entre las funciones A(x) y f(x) es precisamente que f(x) es la derivada de A(x), f(x)=A´(x).

En la relación 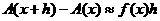, si llamamos a 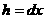, el valor del área  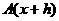queda expresado de la siguiente manera:

 para cualquier x en [a, b]

Y, sumándole al valor del área A(a) todos los valores de las áreas f(x)dx desde a hasta b encontramos el valor acumulado del área A(b):

Por otra parte, la resta A(b)-A(a) determina la acumulación de área cuando x está considerada en el intervalo [a, b]:

Así, la igualdad A´(x)=f(x) relaciona la derivada y la integral expresada por

(La expresión “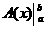” es sólo una notación de la resta 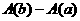. Así cualquier función G(x) que anteceda a la barra “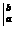”, con los valores a y b, indica que hay que evaluar la función G(x),respectivamente, en a y b: G(a) y G(b) y efectuar la resta G(b)-G(a)).

Por la expresión 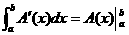, tiene sentido pensar a la integral como la “operación inversa de la derivada”; ya que al integrar una función dada f(x), se obtiene la función F(x) cuya derivada es la función dada: F´(x)=f(x). La función f(x), en la expresión de la integral, implícitamente es la derivada de otra función F(x). Así, a la función F(x) se le conoce como función primitiva;

Función primitiva = integral de su función derivada.

Una vez establecida la relación entre la derivada y la integral, la integral adquiere un carácter operacional, el cual consiste en hallar funciones primitivas a partir de su función derivada.

Conociendo la función primitiva y su derivada en forma explícita se puede construir una tabla de integración, para determinar algunas fórmulas de integración que facilitan cálculos de integrales. Sin embargo, recordemos que la derivada de una función constante es cero. Así, para funciones que incluyen términos constantes en sus expresiones, por ejemplo 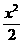, , 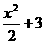 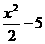resulta que la derivada de cada una de estas es la función f(x)=x. Esto quiere decir que la función primitiva de f(x)=x puede ser cualquiera de las tres funciones, de hecho cualquier función 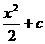, donde c es cualquier constante, es también una función primitiva de f(x)=x. Es preciso, entonces, que al hallar una función primitiva se le añada una constante C.

Observa, además, que la derivada de la primitiva F(x)+c es f(x):

Tabla I

Derivada de F(x)	Función F(x)
	si
	si
1
	si

En la Tabla I se muestran las primitivas de algunas funciones (f(x)), se puede comprobar que al derivar F(x) obtenemos f(x).

Por medio de la Tabla I y la expresión de la integral

se determinan las siguientes fórmulas de integración:

Tabla II: fórmulas de integración

1.      

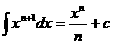
2.      

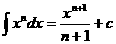
3.      

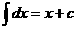
4.      

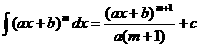
Contamos, hasta ahora, con diferentes expresiones de la integral, donde la característica esencial consiste en los límites de integración;

 (sin límites de integración) y

, donde , para  (con límites de integración)

Ambas expresiones están relacionadas por la función primitiva F(x) y la función derivada F´(x):

 y 

sin embargo la primera expresión determina una función, mientras que la segunda determina un número.

Ejemplo 4.1. Aplicar las reglas básicas de integración

Integral dada	Reformular	Integrar	Simplificar

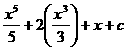Ejemplo 4.2. Consideremos la función 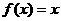 y calculemos las integrales  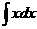y .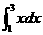

Solución:

De acuerdo a la fórmula de integración

la integral 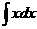 es igual a la función 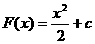, es decir,  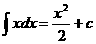(función).

1. Iniciamos con una función f(x)=x. 2. Integramos  y resultó la función  3. Observamos que la derivada de F(x) es f(x)=x.

Para calcular la integral 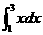 necesitamos la función primitiva, que en este caso es  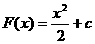y de este modo sólo se requiere calcular la resta  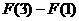ya que la constante se anula, es decir,

;

 (número)

Las expresiones simbólicas de la integral

 y

, donde , para 

relacionan a las funciones primitiva y derivada bajo la siguiente secuencia de funciones (las flechas “®” indican las aplicaciones de dos operaciones: derivada e integración):

función F(x) ® función derivada F´(x) ® función primitiva F(x)+c

La expresión simbólica con límites de integración 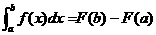 se conoce como integral definida y la expresión simbólica sin límites de integración  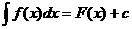se conoce como integral indefinida.

TOMADO DE: http://curso.unach.mx/~msolis/cintegral/La_integral_como_limite.htm