El cálculo integral tiene una estrecha relación con el concepto de área bajo la curva. Es conveniente, entonces, presentar algunas características de esa área que le darán sentido a la relación, donde el aspecto principal consiste en medir el área de una región acotada (Figura 1.1). Y, para poder realizar la medición es necesario establecer un procedimiento general y eficiente.

Figura 1.1
Medir el área a través de otra conocida, es un procedimiento natural y la humanidad ha dado muestra de ello, derivándose, sin embargo, diferentes estrategias para llenar la región acotada.
Poe ejemplo, para medir el área de la región acotada que aparece en la Figura 1.1, se persigue la idea de “transformar” (→) la región en un rectángulo cuya área es conocida: área = base x altura (Figura 1.2).
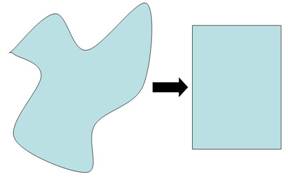
Figura 1.2
Una de las estrategias más comunes consiste en insertar en la región acotada una figura geométrica de área conocida (por ejemplo un rectángulo o un triángulo) de un tamaño tal que cubra lo más que pueda la región acotada (Figura 1.3). Después para las partes restantes, no cubiertas con la figura geométrica insertada, se repite el mismo proceso, pero con figuras geométricas más pequeñas hasta llenar completamente la región y, finalmente, sumar todas las áreas de las figuras geométricas.
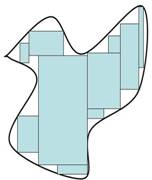
Figura 1.3
Otra estrategia consiste en llenar la región a través de una red cuadriculada (Figura 1.4), en donde cada “cuadrito” representa una unidad. Entonces, para medir el área de la región bastará contar los “cuadritos” insertados.
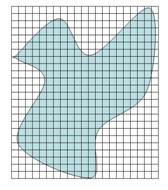
Figura 1.4
Ahora bien, el área bajo la curva (Figura 1.5) es el área de una región acotada asociada a una función. La región está acotada a la derecha por la recta x = a, a la izquierda por la recta x = b, por abajo por el ejex y por arriba por la función positiva f(x) (f(x) > 0), con respecto al sistema de coordenadas cartesianas.
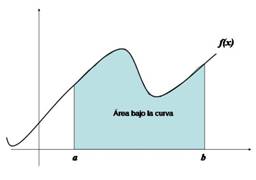
Figura 1.5
El procedimiento para la medición del área, descrito en las estrategias anteriores, es reinterpretado ante esta región acotada. Esta región es orientada por los ejes coordenados, es decir, el eje x da cuenta de la base, mientras que el eje y de la altura: y = f(x) (Figura 1.6).
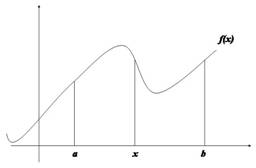
Figura 1.6
Así, para encontrar el valor numérico del área, se requiere considerar figuras geométricas de áreas conocidas que llenen la región. Los rectángulos, como el la Figura 7, y las suma de sus áreas resultaría, aproximadamente, en el valor numérico del área.
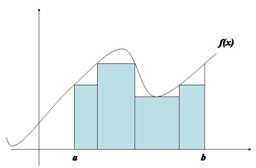
Figura 1.7
Efectivamente, habría que precisar lo que se debe entender como “valor aproximado del área”, es decir, ¿cuándo tenemos una “buena” aproximación al área de la región?
Aproximación al área bajo una curva.
Calcular cada una de las áreas de los rectángulos, que llenan la región acotada para alcanzar el valor del área, necesariamente lleva a precisar el sentido de la aproximación.
Consideremos algunas funciones e intentemos calcular, con el procedimiento anterior, las áreas bajo las curvas respectivas.
Por ejemplo, consideremos la función constante f(x) = k en el intervalo [a, b], el área coincide con el área de un rectángulo. De acuerdo con la Figura 2.1 el área estaría expresada por la fórmula conocida: base por altura = (b – a)k.
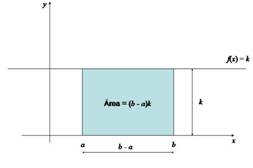
Figura 2.1
Si llevamos a cabo el procedimiento de llenar la región por medio de rectángulos llegaríamos a la misma fórmula conocida. En esta región no importa el tamaño de los rectángulos para alcanzar el área real de la región, como se ve en la Figura 2.2.
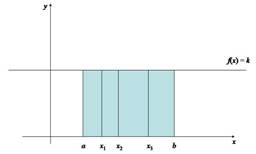
Figura 2.2
Dividamos el intervalo [a, b] en subintervalos mediante los puntos 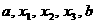 , cada rectángulo tiene la misma altura k y la suma de sus áreas se expresa de la siguiente manera,
, cada rectángulo tiene la misma altura k y la suma de sus áreas se expresa de la siguiente manera,
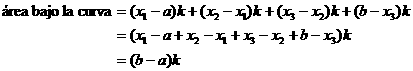
Si dividimos el intervalo [a, b] en n subintervalos iguales, obtenemos el mismo resultado, en este caso la longitud de cada subintervalo es 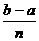 y contamos con n rectángulos. Siendo así, la suma de todos los rectángulos tiene n términos iguales, entonces basta multiplicar n veces el área de un rectángulo,
y contamos con n rectángulos. Siendo así, la suma de todos los rectángulos tiene n términos iguales, entonces basta multiplicar n veces el área de un rectángulo,
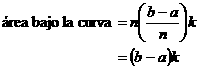
Sin embargo, si consideramos el área bajo la curva formada por la función 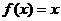 en el intervalo [a, b] (Figura 2.3), la situación del cálculo del área no va a ser exactamente la misma que en el caso anterior.
en el intervalo [a, b] (Figura 2.3), la situación del cálculo del área no va a ser exactamente la misma que en el caso anterior.
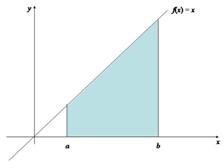
Figura 2.3
Efectivamente, el área puede ser calculada sumando el área del rectángulo y la del triángulo (Figura 2.4)
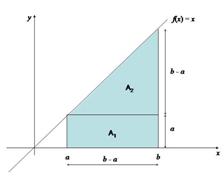
Figura 2.4
y
luego,
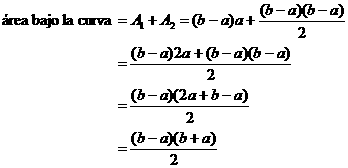
También se podría calcular el área directamente por ser la región bajo la curva un trapecio, su área sería la semisuma de las bases multiplicada por la altura:
Tomemos casos particulares para esta área y observemos los valores numéricos. Por ejemplo, consideremos el intervalo [1, 3] y dividámoslo en tres subintervalos de diferente longitud, como en la Figura 2.5.
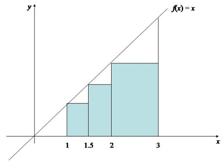
Figura 2.5
Las alturas de los rectángulos son consideradas de tal suerte que todos quedan inscritos en la región acotada, es decir, los rectángulos están por debajo de la curva 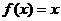 . Y la suma de las áreas de los tres rectángulos resulta:
. Y la suma de las áreas de los tres rectángulos resulta:
(1.5 – 1)1 + (2 – 1.5)1.5 + (3 – 2)2 = 3.25
(Observa que las alturas de los rectángulos 1, 1.5 y 2, son calculadas al evaluar la función 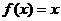 en los extremos izquierdos de los subintervalos correspondientes:
en los extremos izquierdos de los subintervalos correspondientes: 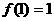 ,
, 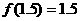 y
y 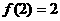 )
)
Por otra parte, si consideramos ahora las alturas de los rectángulos (con las mismas bases del caso anterior), de tal suerte que los rectángulos quedan circunscritos a la región como se presenta en la Figura 2.6.
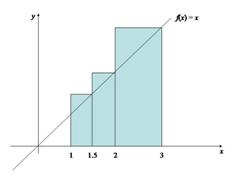
Figura 2.6.
La suma de las áreas de los rectángulos circunscritos resulta ser,
(1.5 – 1)1.5 + (2 – 1.5)2 + (3 – 2)3 = 4.75
(En el mismo sentido que la observación anterior las alturas de los rectángulos son calculadas al evaluar en la función los valores extremos derechos de los subintervalos correspondientes)
Sin embargo, el valor real del área de la región acotada usando la relación encontrada anteriormente, resulta ser,
Este valor se encuentra acotado por los dos valores anteriormente calculados
en este sentido 3.25 y 4.75 son valores aproximados al valor real del área, 4.
La aproximación anterior puede ser mejorada si llenamos la región con rectángulos de tamaño tal que el área que sobrepase a la curva sea considerablemente muy pequeña en comparación con el área que no la sobrepasa.
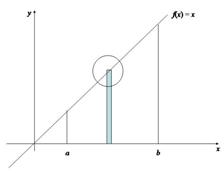
Figura 2.7
Para ilustrar esta observación consideremos nuevamente la región de la Figura 2.3 y al intervalo [a, b] dividámoslo en n partes iguales mediante los puntos
Cada subintervalo es de la misma longitud 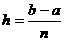
Entonces cada punto puede ser expresado de la siguiente manera:
y la suma de las áreas de los rectángulos que llenan la región de la Figura 2.8 es expresada por
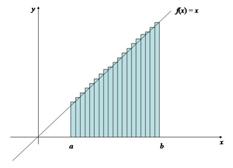
Figura 2.8
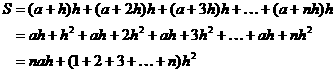
Usando el resultado 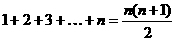
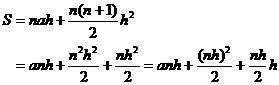
Como 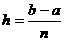 , sustituimos nh por b – a.
, sustituimos nh por b – a.
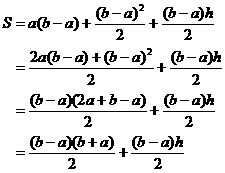
Si h es muy pequeño, esto es, si dividimos al intervalo [a, b] en un número de partes iguales con n muy grande, entonces 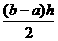 será muy pequeño, también, y la suma de las áreas de los rectángulos circunscritos estará muy próxima al área bajo la curva
será muy pequeño, también, y la suma de las áreas de los rectángulos circunscritos estará muy próxima al área bajo la curva 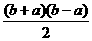 .
.

No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.