LA HORA PUBLICITARIA (PROBLEMA)

Es un hecho muy conocido que la hora marcada en la propaganda de los relojes de pulsera, siempre es
las 10 y 10 minutos. El tema ha motivado incluso consultas en la sección de cartas a los periódicos, a
las que han correspondido los relojeros apelando a razones de estética.
Será. Pero a nosotros matemáticos, esto nos plantea de inmediato el Problema número 1: ¿Qué hora
deberá marcar exactamente el reloj para que los ángulos de horario y minutero respecto a las 12 h sean
iguales?
Este problema es fácil. Pero puede plantearse uno más laborioso. A veces el reloj incluye segundero, y
en este caso éste marca las 6 aproximadamente (los 30s), de modo que los ángulos de las tres agujas
son aproximadamente iguales, de unos 120º. No es difícil demostrar que no pueden ser
matemáticamente iguales a 120º. Pero ahí viene el Problema número 2: ¿Cuál es la hora que deberá
marcar el reloj para que los tres ángulos se aproximen más a 120º? Entendemos por "aproximarse
más" que la suma de las diferencias en valor absoluto de cada ángulo con 120º sea lo menor posible.

SOLUCIONES

Problema número 1.
Si llamamos x al ángulo que el horario forma con la línea de las 10 h, el que el minutero formara con las 12 h será 12x, pues el minutero avanza 12 veces más aprisa que el horario. Siendo el ángulo entre las 10 y las 12 de 60º, la ecuación es obvia: 
12x = 60 - x 
 De donde resulta x = 60/13 de grado. Puesto que 360º corresponden a 12 h, el ángulo equivale a 2/13  de hora. Es decir, que la hora marcada por el reloj es 10h 9m 13s 11/13. 

Problema número 2.
Si el ángulo entre el horario y el minutero fuera exactamente de 120º, por consideraciones similares obtenemos que el ángulo x vale en este caso 60/11 de grado, es decir, que el reloj marcaría las 10h 10m 54s 6/11. Pero entonces el segundero marcaría unos 54 s, muy lejos de los 30s. Se concluye que el punto óptimo que buscamos ha tenido lugar hace aproximadamente medio minuto. 
Supongamos ahora que el ángulo del horario con las 10h es x - ε . Recordando que el segundero va 60 veces más aprisa que el minutero, los valores quedan ahora convertidos en: 
● Ángulo del horario: 60/11 - ε
● Ángulo del minutero: 720/11 - 12ε
● Ángulo del segundero: 60(720/11 - 12ε ) = 43200/11 - 720ε mod 360 = 43200/11 - 3600 - 720ε
= 3600/11 - 720ε
Del ángulo del segundero hemos restado un número suficiente de circunferencias, concretamente 10, o sea 3600º, para conseguir que el valor final sea inferior a 360º. 
En primera aproximación, podemos concluir que ε deberá ser del orden de medio minuto horario (o sea unos 3º). Veamos los ángulos entre las respectivas manecillas. 

• Ángulo horario-minutero: 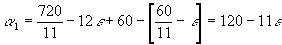 (obvio)
• Ángulo minutero-segundero:
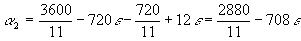
• Ángulo segundero-horario: 

 Ahora se trata de hallar el mínimo de la suma: 
 
 
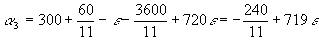
Unos tanteos rápidos concluyen que el mínimo se alcanza cuando el tercer paréntesis se anula, o sea para e = 1560/7909 grados. Con lo cual el ángulo buscado vale: 
  

x = 41580/7909 grados. Este ángulo equivale a 1386/7909 de hora. O sea que son las: 
:
  10^h 10^m 30^s 630/719 

 Como se ve, el resultado es de lo mas preciso. Los ángulos valen: 
 
a ₁ = 117,83º
a ₂ = 122,17º
a ₃ = 120,00^o 
tomado de:    http://www.mensa.es/juegosmensa/s111115.html#SOLU111