FRACCIONES
1
. CONCEPTO:
Una fracción es considerada la parte o
partes de un todo dividido en varias iguales.
Pero también es la relación de dos
cantidades: el denominador, que indica en cuantas partes iguales se ha dividido
“todo” y el numerador que determina cuántas se han considerado.
Haciendo un alcance más, la fracción
también es una división de dos números, cuyo resultado es un número decimal.
Esta idea es la que se va a utilizar para el desarrollo de operaciones entre
fracciones.
2 OPERACIONES CON FRACCIONES:
A) IDEA DE NÚMERO MIXTO:
A) IDEA DE NÚMERO MIXTO:
Ahora lo que indica el denominador es que se divida “todo” en cinco
partes iguales y se tomen nueve y en este caso se necesitan 2 figuras divididas
en cinco partes iguales cada una y de las cuales, para tomar nueve, se han
pintado una totalmente y de los otros cuatro rectángulos pequeños, es decir:
4/5 de ella.
Ahora podemos ver una equivalencia importante:
El método operativo es más sencillo de aplicar, para realizar la
conversión en uno u otro sentido:
B) ADICIÓN
Y SUSTRACCIÓN DE FRACCIONES:
La adición de fracciones tiene métodos que hay que saber cuál utilizar
según los términos que se están operando.
PRIMER CASO
Por ejemplo:
Si son dos fracciones con numeradores y denominadores menores que 10 es
más fácil y práctico usar el método del aspa:
SEGUNDO CASO
Hay
casos en que tenemos o podemos simplificar a una fracción equivalente, esto
sucede cuando los denominadores de las fracciones tienen un factor o factores
en común.
Por ejemplo:
dividimos numerador y denominador entre 4 y se obtiene:
TERCER CASO
También se puede presentar que podemos convertir el resultado a
número mixto
Por ejemplo:
CUARTO CASO
Si son dos fracciones con denominadores con varios factores en común es mejor utilizar el Método el Mínimo Común Múltiplo, cuyo objetivo es que las dos fracciones tengan el mismo denominador, en otras palabras, sean homogéneas.
Por
ejemplo:
si nos damos cuenta el primer denominador
ha sido multiplicado por 5 y para obtener una fracción equivalente también
debemos multiplicar por 5 a su numerador, es decir, se tendría: 5 x 7 = 35.
Para la segunda
fracción el denominador ha sido multiplicado por 2 entonces a su numerador lo
multiplicamos por 2, finalmente tendríamos las dos siguientes fracciones:
¿Qué pasaría si lo
calculamos por el método el aspa?
ambos términos del
resultado tienen factor 3 y 5 que podemos simplificar así:
El método del MCM es el
más general y sirve cuando se tienen más de dos fracciones cuyos denominadores
tienen factores comunes entre todos o parcialmente entre algunos.
Por ejemplo
Para el caso de
sustracción como se trabajan dos fracciones, se aplica los casos mencionados,
según convenga:
Por
ejemplo:
Para el siguiente
ejercicio aplicamos el método del MCM:
C) MULTIPLICACIÓN DE FRACCIONES:
La multiplicación es más sencilla, porque se multiplica numerador con
numerador y denominador con denominador.
Por ejemplo:
Si se multiplica una fracción con un número entero este número
se considera con denominador 1.
Por ejemplo:
El
resultado ha sido simplificado, ese proceso de simplificación se pudo haber
realizado al inicio de la operación:
dividimos
entre cuatro al valor entero y al denominador. La simplificación, en la
multiplicación de fracciones, siempre se realiza entre términos que se
encuentran en el numerador y el denominador.
D) DIVISIÓN DE FRACCIONES:
Para dividir fracciones se pueden usar cualquiera de estos métodos:
Primer método: Se multiplica como
indican las flechas y se colocan los resultados según lo indicado
Segundo método: Se invierte
la segunda fracción (divisor) y se procede como si fuese una multiplicación.
Tercer método: Se procede según
las flechas:











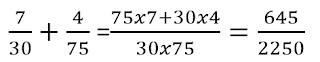









No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.