lunes, 28 de noviembre de 2016
sábado, 26 de noviembre de 2016
domingo, 2 de octubre de 2016
LOS SISTEMAS DE NUMERACIÓN
LOS SISTEMAS DE
NUMERACIÓN
Para representar un número
necesitamos un sistema, que, mediante ciertas reglas y principios, permitan
hacerlo adecuadamente. Es por eso que ahora aprenderemos como a partir de la
idea Inicial, lograremos simbolizarlo.
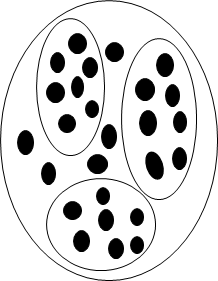
Tenemos el siguiente gráfico:
Si nos preguntan
cuántos elementos tiene, lo prmero que hacemos es contar y de ese conteo obtenemos 26 que es la
representación simbólica del total de
elementos.
La pregunta es
¿porqué 26? es decir, ¿porqué 2 y 6 juntos?
La respuesta es
que se está usando el sistema decimal de base 10 para representar esta
cantidad, mejor dicho, se agrupan los elementos de 10 en 10 (valor de la base)
y vamos a obtener 2 grupos completos
de 10
y 6 elementos sobrantes.
Considerando este razonamiento si los mismos elementos lo representásemos en el sistema de base 7 en tonces la agrupación quedaría así: 3 grupos completos de 7 elementos y 5 elementos sueltos y su representación sería 35 en el sistema de base 7 o abreviado: 357
Esto nos lleva a deducir el método para poder representar un número en cualquier sistema de numeración, ya que si hablamos de “agrupar” entonces es fácil saber que, la operación correspondiente es la DIVISIÓN entonces nos falta
saber que hacemos si la cantidad de “grupos” es mayor que el valor de la
base del sistema de numeración, veamos el mismo ejemplo pero usando el sistema
de base 3 , se tendría 8 grupos y 2 elementos sueltos,entonces se agruparía
así:
Entonces se escribiría así:
2 “grupos grandes”
2 “grupos medianos”
2 “elementos sueltos”
El numeral sería:
222(3)
El agrupar nos lleva a la
Operación de DIVISIÓN
Tomamos el último cociente y todos
los residuos anteriores entonces: 222(3)
En conclusión:
26 del sistema de base 10 se puede
representar como: 35(7) y 222(3)
26 =35(7) = 222(3)
Ahora como comprobamos que: 35(7) y 222(3)
son iguales a 26, la lógica nos dice que para llegar a la representación
en base 7 y base 3 hemos dividido y en ese proceso de la división también se ha
restado, lo único que debemos hacer es usar las operaciones contrarias, es
decir,multiplicación y adición y lo haremos de la siguiente manera:
- Colocamos las cifras del número separadas y la base en la parte inferior izquierda en esta disposición:
- Luego bajamos la primera cifra de la izquierda para empezar con las operaciones antes mencionadas (Multiplicación y adición):
El número obtenido es 26, con el cual hemos realizado los ejercicios
anteriores.
Así es el método de Ruffini, que lo
hemos deducido desde la noción inicial, pero no es el único también podemos
utilizar la descomposición polinómica que es una forma abreviada del método
de Ruffini:
Se multiplica cada cifra por el valor de la base y cada base tendrá un
exponente, empezando con cero para la base que multiplica a la última cifra y
sucesivamente colocamos: 1;2;3;…..como exponente para cada base que multiplica a las cifras
que se encuentran a la izquierda de la última:
222(3) = 2x32+2x31+2x30
Entonces:
- Para convertir un número del sistema de base 10 a otro sistema dividimos en forma sucesiva
- Para convertir un número de un sistema de base cualquiera a base 10 lo que podemos aplicar es el Método de Ruffini o la descomposición Polinómica
Ahora la última pregunta: ¿Y si queremos convertir un número de un
sistema diferente de base 10 (o sistema decimal) a otro también diferente de
base 10?
La pregunta es sencilla de responder si analizamos los casos anteriores:
- Tenemos el número escrito en una base” m” (diferente de 10) y queremos pasarlo a base “n” (también diferente de 10)
- Primero, el número de base “m” lo pasamos a base 10 por Ruffini o descomposición polinómica.
- Segundo, el resultado obtenido en base 10 lo convertimos a base “n” por divisiones sucesivas.
Ejemplo:
Convertir: 164(7) al sistema de base 4
Primero: 164(7) a base 10
164(7) = 1x72+6x71+4x70=
49+42+4= 95
Segundo: 95 a base 4
sábado, 24 de septiembre de 2016
DESCOMPOSICIÓN DE UN NÚMERO COMPUESTO EN FACTORES PRIMOS Y CANTIDAD DE DIVISORES
DESCOMPOSICIÓN DE UN
NÚMERO COMPUESTO EN FACTORES PRIMOS Y CANTIDAD DE DIVISORES
Los números primos son aquellos que solo son divisibles
entre 1 y él mismo número, esto sucede en el campo de los números naturales.
Pero hay números que tienen más de dos divisores y estos son los números
compuestos; también hay que considerar al uno, que escapa de éstas dos ideas.
Entonces la clasificación más común es la siguiente:
Los números primos: 2;3;5;7;11;13;17;19;23;29;31;37;41;43;47;53;59;61;67;71;73;79;83;89;97;101;103;
107; …
La importancia de los números primos es que nos permiten
expresar un número compuesto, es decir, podemos representar un número compuesto
en función de sus factores primos.
Esta forma de expresar los números compuestos tiene como
base dos aspectos importantes que hay que conocer: los criterios de divisibilidad y leyes de exponentes.
Por ejemplo:
Para descomponer el
número 360 y expresarlo en sus factores primos, tenemos que considerar los
criterios de divisibilidad por dos (porque la última cifra es cero), por tres
(porque la suma de sus cifras es múltiplo de tres) y por cinco (porque la
última cifra es cero).
Ya tenemos expresado a 360 en función de sus factores primos
con esta descomposición podemos determinar la cantidad de divisores que tiene y
cuáles son:
TABLA DE DIVISORES
Para construir la tabla de divisores primero tomamos las
potencias sucesivas del factor con mayor exponente obtenido en la
descomposición, en el ejemplo sería 23 y se haría lo siguiente:
20;
21 ;22 ;23 y
los otros factores de la misma forma, pero sin el exponente cero, luego lo
disponemos de la siguiente forma: se colocan líneas divisorias para cada
sucesión de potencias de cada factor primo diferente
Se multiplican los números que están en el lado vertical con
cada fila, pero considerando solo las filas por encima de la línea divisoria:
En el ejemplo las potencias del tres solo se multiplicarán
con las potencias del factor 2 y las potencias del factor 5 se van a
multiplicar con las tres filas que se encuentran por encima de su línea
divisoria, así como indica los gráficos anteriores.
Podemos
ver fácilmente que la cantidad de divisores de 360 es 24, es decir, que hay 24
números que dividen exactamente a 360, pero existe otra forma para calcular la
cantidad de divisores de 360, sin usar la tabla de divisores:
· ¿Cuántos divisores pares, tiene 360?
Viendo la tabla de divisores contamos 18 divisores pares:
2;4;6;8;10;12;18;20,24;30;36;40;60;72;90;120;180 y 360
La otra forma sería la siguiente:
360= 2x2x2x3x3x5=
2(22x 32x
51) colocamos
el 2 delante de los
otros factores para obtener todos los divisores múltiplos de dos (o sea pares)
ahora aplicamos la fórmula a los factores dentro del paréntesis: (2+1) (2+1) (1+1) = 3x3x2 =18 divisores
·
¿Cuántos divisores múltiplos de 5,
tiene 360?
Mirando la tabla tenemos: 5;10;15;20;30;40;45;60;90;120;180
y 360 en total 12 divisores múltiplos de 5. Ahora:
360= 2x2x2x3x3x5=
5(23x 32)
aplicamos la fórmula para los términos dentro del paréntesis: (3+1) (2+1) = 4x3=12
·
¿Cuántos divisores cuadrados
perfectos, tiene 360?
En la tabla: 1;4;9 y 36 son cuatro divisores cuadrados
perfectos. Aplicando la fórmula sería así: se expresan los factores primos de
la descomposición con exponentes 2 (aquellos que se puedan)
·
¿Cuántos divisores impares, tiene
360?
Esto se resuelve considerando el total de divisores y la
cantidad de divisores pares:
domingo, 18 de septiembre de 2016
lunes, 12 de septiembre de 2016
EL MÁXIMO COMÚN DIVISOR Y EL MÍNIMO COMÚN MÚLTIPLO
EL MÁXIMO COMÚN
DIVISOR
Se presenta el siguiente problema:
“Un alcalde establece colocar postes
igualmente distanciados alrededor de un terreno rectangular cuyas dimensiones
son: 560 metros de largo y 240 metros de ancho. Además debe colocarse un poste en
cada esquina y el número de postes debe ser el menor posible; con estos datos,
¿cuántos postes deberá mandar a colocar el alcalde alrededor del terreno?”
Al analizar el problema consideremos algunas condiciones
importantes para encontrar la solución.
Primero: “…postes igualmente distanciados...” significa que es una
longitud que divide exactamente al largo como al ancho del terreno, es decir,
es “divisor de 560m. y 240m. al mismo
tiempo (común)”.
Segundo: “…debe colocarse un poste en cada esquina…” esto es importante
para el conteo final de postes, para no contar dos veces, sobre todo aquellos
que están en las esquinas.
Tercero: “…el número de postes debe ser el menor posible…” este es el
dato final, si queremos usar el menor número de postes alrededor del terreno,
entonces el distanciamiento entre dos postes, debe ser el mayor posible, en
otras palabras: “el máximo”.
Conclusión: la
longitud entre poste y poste divide exactamente al largo y ancho del terreno,
es decir, es un divisor común, además es
máximo, finalmente lo que debemos calcular es el Máximo Común Divisor de 560 y 240: MCD (560;240)
- MÉTODOS DE CÁLCULO DEL MCD:
A)
Considerando los divisores de cada número:
560:
1;2;4;5;7;8;10;14;16;20;28;35;40;56;70;80;112;140;280;560
240:
1;2;3;4;5;6;8;10;12;15;16;20;24;30;40;48;60;80;120;240
Divisores comunes: 1;2;4;5;8;10;16;20;40 y 80
El Mayor de ellos es: 80, entonces el MCD (560;
280) = 80
B)
Descomposición Individual:
Se descompone canónicamente cada número, es decir, en base a sus factores
primos:
560 =24x5x7
240= 24x3x5
Ahora consideramos solo los factores que son comunes, con sus menores
exponentes (si hay factores primos, comunes, pero con diferentes exponentes):
MCD (560;240) = 24x5 = 80
C)
Descomposición Simultánea:
Se descomponen los números al mismo tiempo, pero solo consideramos los
divisores que dividen exactamente a los números simultáneamente.
MCD (560;240) =
2x2x2x2x5= 80
D)
Algoritmo de Euclides:
Se
usa cuando es difícil saber qué factores comunes tienen los números y se basa
en dividir los números en cuestión, hasta obtener un residuo igual a cero,
colocando los cocientes y residuos de la siguiente forma:
MCD
(560;240) = 80
¿pero qué es el Máximo Común Divisor?, es
un número, no un método ni un procedimiento, simplemente un número, que divide
exactamente a otros al mismo tiempo y es el de mayor valor posible.
Finalmente, al resolver el problema:
Cada poste debe estar distanciado del otro,
80 metros, por lo tanto, en el largo del terreno hay 560:80 = 7 espacios y entre cada espacio hay dos postes,
finalmente en cada largo, considerando las esquinas, tenemos 8 postes, en total 16.
En el ancho algo similar: 240:80 = 3 espacios, por lo tanto,
habría 4 postes, pero estamos considerando los que están en las esquinas, que
ya han sido contados; como son dos esquinas restamos dos postes y nos quedamos
con solo dos para cada ancho, en total 4.
Sumando todo tendríamos: 20 postes en total.
EL MÍNIMO COMÚN MÚLTIPLO
Tenemos el siguiente problema:
“Se tiene cierta cantidad de
ladrillos de dimensiones: 0,3m de largo, 0,05 m de grosor y 0,08m de alto; con
la menor cantidad de ellos, se quiere construir un cubo de este material,
¿cuántos ladrillos serán necesarios teniendo en cuenta las dimensiones de los
ladrillos?”
Analicemos el problema:
Primero: el cubo
tiene sus tres dimensiones iguales (largo, ancho y altura) entonces la longitud
del lado del cubo (arista) es el mismo en cada dimensión.
Segundo: La
longitud de la arista del cubo se forma con cada dimensión del lado del
ladrillo, en otras palabras, esta longitud debe contener exactamente a cada
dimensión del ladrillo, es decir, debe ser “un
múltiplo” de cada longitud del ladrillo.
Tercero: Se debe
usar el menor número de ladrillos, y eso significa que la longitud de la arista
del cubo es la menor posible, “mínimo”.
Conclusión: La
longitud de la arista del cubo “deber
mínima y un múltiplo de las dimensiones del ladrillo” por lo tanto el Mínimo Común Múltiplo de: 0,3m de
largo, 0,05 m de grosor y 0,08m de alto en centímetros: 30 cm.,5 cm. y 8 cm.
(solo se multiplica por 100 a cada uno) :
MCM (30;5;8)
- MÉTODOS DE CÁLCULO DEL MCM:
A)
Descomposición Individual:
Se descompone canónicamente cada número, es decir, en base a sus factores
primos:
30 = 2x3x5
5 = 5
8 = 23
Ahora consideramos todos los factores comunes y no comunes con sus
mayores exponentes:
MCM (30;5;8) = 23x3x5 =
120 cm.
B)
Descomposición Simultánea:
Se
descomponen los números al mismo tiempo, y consideramos factores primos comunes
y no comunes hasta llegar a 1.
Finalmente,
al resolver el problema:
La
longitud de la arista del cubo debe ser 120 cm. para calcular el número de
ladrillos se realiza la siguiente operación:
sábado, 3 de septiembre de 2016
RECOPILACIÓN DE TRUCOS OPERATIVOS MATEMÁTICOS
RECOPILACIÓN DE
TRUCOS OPERATIVOS MATEMÁTICOS
1.
COMO USAR EL COMPLEMENTO ARITMÉTICO
PARA MULTIPLICAR.
Recordemos como se calcula el complemento
aritmético en base decimal de un número:
CA (2376) = 10000 – 2376= 7624
Para las dos primeras cifras del resultado
sumamos los dos CA, es decir, 9+6 = 15
y se
resta de 100 tenemos: 100-15= 85 son las dos primeras cifras.
Para las dos últimas cifras del resultado
se multiplican los dos CA, entonces: 9x6=54
son las dos últimas cifras del resultado
cuyo valor completo es 8554
2.
MÉTODO RUSO PARA MULTIPLICA
Para aplicar este método primero debemos seguir las
siguientes reglas para cada situación
Primer caso:
Tomemos dos números, al primero (puede ser cualquiera de los
dos, pero para tener un orden elijamos al primero) se le duplica sucesivamente
y al segundo factor se le divide entre dos.
Ejemplo
Al momento que este proceso termina, es decir, ya no podemos
dividir entre dos (división entera), vamos a fijarnos en aquel resultado o resultados
que se encuentran frente a un valor impar y posteriormente se suman; en el
ejemplo el único valor que está frente a un valor impar es 720 (frente a 1),
por lo tanto, este es el producto resultante.
Segundo caso:
¿Qué sucede si en la columna que dividimos entre dos, hay
algún resultado impar?
La respuesta sería que a este número impar le restamos 1 y
procedemos a dividirlo entre dos.
Igual que el caso anterior consideramos los números frente a
las cantidades impares para luego sumarlos.
Ejemplo
En el ejemplo los únicos valores frente a números impares son
78 (que está frente a 17) y 1248 (que está frente a 1), entonces: 1248 + 78 =
1326
3.
MÉTODO EGIPCIO PARA MULTIPLICAR:
Sin quererlo ahora mostraremos un método basado en el sistema
binario, la explicación quedará para luego en otro momento, por ahora veremos
cómo se usa el método.
Ejemplo:
Para verificar la certeza del método usaremos el ejemplo
anterior: 39 x34.
En este caso en vez de 34 colocaremos 1 y ambos términos (34
y 1) se irán duplicando y nos detendremos antes que el valor que estamos
obteniendo al duplicar el 1, supere al valor que está reemplazando (en este
caso 34)
En la columna donde está el 1, buscamos aquellos valores que
sumados nos dan exactamente 34, para el ejemplo que desarrollamos estos valores
son 32 y 2 (32+2=34)
Luego vemos que
cantidades están frente a estos dos valores (32 y 2)
Y verificamos que son:
1248 y 78; finalmente sumamos estos valores
1248+78 = 1326 y
obtenemos el resultado final
4.
MÉTODO HINDÚ PARA MULTIPLICAR:
Ejemplo 1:
Multipliquemos 405 x 32
Para aplicar este método primero dibujamos una tabla con un número de
filas igual a la cantidad de cifras que tiene el multiplicador (en este ejemplo
es el número 32 por lo tanto 2 filas) y un número de columnas igual a la
cantidad de cifras que tiene el multiplicando (en el ejemplo que hemos elegido
es 405, por lo tanto, serán 3 columnas), además trazamos las diagonales como
indica el gráfico de la siguiente manera:
Colocamos los números que se multiplican de la siguiente
forma:
Multiplicamos 4x3=12
4x2= 8 y colocamos las cifras de cada resultado en el casillero
correspondiente de la siguiente forma:
Continuamos con las
demás multiplicaciones: 0x3=0 0x2=
0 5x3 =15 5x2 =10
Y terminamos de completar la tabla
obteniendo finalmente la siguiente:
Para finalizar hacemos la suma de los resultados
como indica las flechas, obteniéndose finalmente:
El resultado es considerando los valores que se han obtenido,
es decir: 12960
Ejemplo 2:
536 x 47
En este caso
cuando una suma sale mayor que diez se hace los siguiente:
Finalmente tenemos:
La respuesta
es: 25192
Suscribirse a:
Comentarios (Atom)
Archivo del blog
-
►
2017
(19)
- ► septiembre (1)
-
►
2014
(441)
- ► septiembre (61)
-
►
2011
(38)
- ► septiembre (4)
-
►
2010
(74)
- ► septiembre (6)