EJERCICIOS RESUELTOS DE APLICACIONES DE LA DERIVADA E INTEGRAL A LA ECONOMÍA Y ADMINISTRACIÓN
v DERIVADAS
Producción y productividad
- Un estudio de productividad en el turno matinal en una cierta fábrica indica que un trabajador medio que llega al trabajo a las 8.00 a.m. habrá ensamblado
 radio transistores x horas después.
radio transistores x horas después.
¿En que momento de la mañana esta actuando el trabajador con máxima eficacia?
Cantidad de radios producida por hora= 
Para hallar el momento en que es mas eficiente, encontraremos en que hora el trabajador alcanza su mayor nivel de producción, para ello derivaremos la función de producción e igualaremos la primera derivada a cero, mientras que para demostrar que realmente es la máxima producción calcularemos la segunda derivara, la cual debe ser negativa para demostrar el máximo nivel de producción.
t no puede ser -1 ya que el tiempo no se puede expresar en unidades negativas
Ahora comprobaremos que es la máxima productividad..
 y como
y como 
- Un fabricante ha estado vendiendo bombillas a 6 dólares cada una y, a este precio, los consumidores han estado comprando 6,000 bombillas por mes. El fabricante desearía elevar el precio y estima que por cada dólar de incremento en el precio se venderán 1,000 bombillas menos cada mes. El fabricante puede producir las bombillas a un coste de 4 dólares por bombilla. ¿A qué precio debería vender el fabricante las bombillas para generar al mayor beneficio posible?
P1=6 Q1=6000
P2=6+x Q2=6000-1000x C = 4x
Ahora estableceremos la función beneficio la cual la derivaremos para poder calcular el máximo beneficio y si la 2da derivada es negativa comprobaremos lo dicho.
 y
y 
Entonces diremos que el fabricante para obtener más beneficios lo que debe hacer es reducir el precio en 0.002 hasta 5.998
- Un cultivador de agrios de Tambogrande estima que si se plantan 60 naranjos, la producción media por árbol será de 400 naranjas. La producción media decrecerá en 4 naranjas por árbol adicional plantado en la misma extensión. ¿Cuántos árboles debería plantar el cultivador para maximizar la producción total?
Árboles de naranja= AN1= 60 Producción media= PM1 = 400
AN2 = 60 + x PM2 = 400 – 4x
Producción total = PT = (60 + x)( 400 – 4x)
PT = 2400 + 160x – 4x2
Para maximizar PT
PN = 60 + x = 60 + 20 = 80
Oferta y demanda
- Las funciones de oferta y demanda de un cierto articulo son S(p)=4p + 200 y D(p)= -3p +480, respectivamente. Halle el punto de equilibrio y el correspondiente número de unidades ofertadas y demandadas, y dibuje las curvas de oferta y demanda en el mismo conjunto de ejes.
S(p)=4p + 200 D(p)= -3p +480
En punto de equilibrio: S(p) = D(p)


 4p + 200 = -3p +480 7p = 280 p = 40
4p + 200 = -3p +480 7p = 280 p = 40
S(40)=4(40) + 200=360 D(40)= -3(40) +480=360
- Suponga que las funciones de oferta y demanda de un cierto artículo son S(p) = ap + b y D(p) = cp + d, respectivamente.
a) ¿Qué puede decir sobre los signos de los coeficientes a, b, c y d si las curvas de oferta y demanda están orientadas como muestra el siguiente diagrama?
Si S(p) = ap + b tiene el comportamiento de una oferta y considerando que en el eje de las ordenadas se encuentra q y en el de las abcisas p, concluimos que:
a > 0 y b < 0
Mientras que D(p) = cp + d tiene el comportamiento de una demanda, tenemos que:
c < 0 y d > 0
b) Exprese el precio de equilibrio en términos de los coeficientes a, b, c y d.
En equilibrio S(p) = D(p)
 a p + b = c p + d
a p + b = c p + d 
c) Use su respuesta de la parte b) para determinar que le sucede al precio de equilibrio cuando a crece.
Si 
d) Use su respuesta de la parte b) para determinar qué le sucede al precio de equilibrio cuando d crece.
Si 
- 21. La demanda de consumo para un cierto artículo es D(p) = -200p + 12.000 unidades por mes cuando el precio de mercado es de p dólares por unidad.
a) Dibuje esta función de demanda.
b) Exprese el gasto total mensual de los consumidores para el artículo como una función de p. (El gasto total mensual es la cantidad total de dinero gastado por los consumidores cada mes en el artículo.)
GT = p (-200p + 12000)
GT = - 200p2 +12000p
c) Dibuje la función gasto total mensual.
e) Use el gráfico de la parte c) para estimar el precio de mercado que genera el mayor gasto de consumo.
Para determinar con que precio se obtendrá el mayor gasto tendremos que derivar el gasto.
Así también se demuestra en el grafico de c
Costos
- Un camión está alquilado para transportar mercancías desde una fábrica a un almacén. El salario del conductor ha sido fijado por horas y así es inversamente proporcional a la velocidad a la que conduce el camión. La cantidad de gasolina gastada es directamente proporcional a la velocidad a la que conduce el camión, y el precio de la gasolina permanece constante durante el viaje. Demostrar que el coste total es menor a la velocidad para la cual el salario del conductor es igual al coste de la gasolina usada.
Si: salario del conductor :  cantidad de gasolina gastada: G=kv
cantidad de gasolina gastada: G=kv
Precio de gasolina =  =
= coste de la gasolina usada:
coste de la gasolina usada:  .G
.G
Se pide demostrar que cuando el coste total es menor, el salario del conductor es igual al coste de la gasolina usada, cuando la velocidad minimiza el costo.
Es decir que  >0, entonces
>0, entonces  = kv
= kv
 , pero también lo podemos expresar así:
, pero también lo podemos expresar así:  = kv
= kv
Con esto queda demostrado.
- Suponga que el coste total (en dólares) de fabricación de q unidades viene dado por la función C (q) = 3q2 + q + 48.
a. Exprese el coste medio de fabricación por unidad como una función de q.
Cme = 
b. ¿Para qué valor de q es menor el coste medio?
c. ¿Para qué valor de q es igual el coste medio al coste marginal? Compare este valor con su respuesta de la parte b).
Primero hallamos el costo marginal
Ahora igualamos el Cme y el Cmg
Podemos deducir que el valor obtenido es del mismo valor que en la pregunta b), con lo cual se puede deducir que el punto en el que se intercepta el costo marginal con el costo medio es justo cuando el costo medio esta en su mínimo.
d. En el mismo conjunto de ejes represente las funciones de coste total, coste marginal y coste medio.
- Una caja cerrada con base cuadrada debe tener un volumen de 250 metros cúbicos. El material para el suelo y la tapa de la caja cuesta 2 dólares por metro cuadrado y el material para los lados cuesta un dólar por metro cuadrado. ¿Puede construirse la caja por menos de 300 dólares?
V = a2b = 250 ab=250/a
CT = costo de base + costo de lados
CT= s/.2 (2xa2) + s/.1(4xab)
CT= 4a2+2x = 4a2 +
= 4a2 + 
- Una empresa manufacturera recibe un pedido de q unidades de cierto artículo. Cada una de las máquinas de la empresa puede producir n unidades por hora. El costo de puesta en marcha es s dólares por máquina y el costo de operación es p dólares por hora.
a) Obtenga una fórmula para hallar el número de máquinas que deben emplearse para mantenerse costo total lo más bajo posible.
SOLUCIÓN
C total = Costo de puesta en marcha + Costo de operación.
También x = número de máquinas.
El costo de puesta en marcha de es = sx.
Además el costo de operación = k/x.
Nótese que q artículos a n artículos por hora resulta (q art.) / (n art./h) = q/n horas y en p horas qp/n por lo que el costo de operación es =qp/nx.
b) Demuestre que el costo total es mínimo cuando el costo de puesta en marcha de las máquinas sea igual al costo de operación de éstas.
Costo total es entonces = sx + (qp)/(nx) donde la variable independiente es x.
La primera derivada es C' = s - (qp)/(nx²) = 0
qp/nx² = s
qp/nx = sx
es decir que el costo de operación = costo de puesta en marcha
- Una empresa de artículos electrónicos utiliza 600 cajas de transistores cada año. El costo de almacenamiento de una caja durante un año es 90 centavos, y los gastos de envío son $30.00 por pedido. ¿Cuántas cajas debe solicitar la empresa en cada envío para mantener el costo total en un mínimo?
SOLUCIÓN
En 600 cajas a x cajas por pedido el número de pedidos es = 600/x.
Costo de solicitud a $30 cada uno = (30)(600)/x = 18,000/x.
El costo de almacenamiento = (x/2)(.90)= .45x
El costo total es C = .45x + (1800/x).
Su derivada es C = .45 - (1800/x²) = 0
.45x² = 1800
x = sqr(18000/.45) = 200 cajas
Probaremos que este valor hace un mínimo en C:
La segunda derivada es C'' = 36,000/x³ y si hacemos x=200, resulta C'' >0 que es la condición necesaria y suficiente para hacer un mínimo.
- Por medio de sus estaciones autorizadas, una compañía petrolera distribuye 16,000 mapas de carreteras cada año. El costo de poner en marcha una impresora para editar los mapas es $100.00 por cada jornada de producción. Además, los costos de producción son 6 centavos por mapa y los costos de almacenamiento son 20 centavos por mapa al año.
Los mapas se distribuyen a un ritmo uniforme durante el año y se imprimen en lotes iguales, espaciados, de manera que cada uno llega justo cuando el anterior se ha agotado. ¿Cuántos mapas debe imprimir la compañía petrolera en cada lote para minimizar el costo?
SOLUCIÓN
16,000 mapas a x mapas por jornada, resulta un número de jornadas = 16,000/x
Costo de puesta en marcha = 100 (16,000/x) = 1'600,000/x
Costo de producción = (.06) (16,000) = $ 960.00
Costo de almacenamiento = (x/2)(.20) = .1x
Costo total C = 960 + (1'600,000 /x) + .1x
La derivada es C' = 0 - (1'600,000/x²) + .1 = 0
1'600,000 /x² = .1
x = sqr (1'600,000 / .1)
x = 4,000 mapas
- Suponga que el costo total, en dólares, de fabricar q unidades de cierto artículo es
R(q) = -2q²+68q-128
a) ¿En qué nivel de ventas el ingreso medio por unidad es igual al ingreso marginal?
b) Verifique que el ingreso medio sea creciente si el nivel de ventas es inferior al nivel del literal a) y decreciente si el nivel de ventas es superior al del literal a).
Revisaremos si el ingreso medio es creciente o decreciente en un intervalo donde
q es mayor que 8 y q es menor que 8 con la primera derivada del ingreso medio.
SOLUCIÓN DE LA a)
Rm = -2q +68 - (128/q) y además R'= -4q+68
-2q +68 -128/q = -4q +68
2q - 128 /q = 0
2q² = 128, q² = 64
q = 8
SOLUCIÓN DE LA b)
Rm = -2q + 68 -128/q
R'm = -2 + 128 / q² = 0
Probemos para q> 8, digamos 9
R'm (9) = -2 + 128/81 = -2 + 1.58 = cifra negativa, por lo tanto Rm es decreciente.
Probemos para q<8 7="" digamos="" o:p="">
R'm = -2 + 128/49 = cifra positiva, por lo tanto Rm es creciente.
- Suponga que la ecuación de demanda de cierto artículo es q=60-0.1p donde p se halla en el intervalo cerrado-cerrado [0,600].- a) Exprese la elasticidad de la demanda como una función de p; b) Calcule la elasticidad de la demanda cuando el precio es p=200 y explique la respuesta; c) ¿A qué precio la elasticidad de la demanda es igual a -1?
Si q=60-0.1p ; dq/dp = -0.1
SOLUCIÓN
a) elasticidad = (p/q) (dq/dp) = p(-0.1)/(60-0.1p) = -0.1p/(60-0.1p)
b) Cuando p= 200, elasticidad = [-0.1 (200)] / [(60- (.1)(200)] = -20/40 = - 0.5%
c) La elasticidad es -1 cuando -1 = -0.1p / (60 -.1p)
-60 + .1p = -.1p
.2p = 60 ; p = $300
- Suponga que la ecuación de demanda de cierto artículo es q=a/pm, donde a y m son constantes positivas. Demuestre que la elasticidad de la demanda es igual a (-m) para todos los valores de p.
SOLUCIÓN
Usemos q=ap-m cuya derivada sería dq/dp=-amp-m-1.
Así la elasticidad = (p/q) (dq/dp) = (p/ap-m) (-amp-m-1)
elasticidad = (- p amp-m-1) / (ap-m) = -p1-m-1+m a1-1 m = -m p° a° = -m (1) (1) = -m
elasticidad = -m, donde p no tiene restricciones.
- Cuando se producen q unidades de un cierto articulo, el costo total de fabricación es de C( q ) = 3 q3 + 5 q + 75 dólares ¿ A que nivel de producción será menor el coste medio por unidad.?
Costo medio = costo total
Q
|
A ( q ) = C( q ) = 3 q3 + 5 q + 75 = 3q +5 + 75
q q q
El costo medio por unidad mínimo cuando se producen 5 unidades.
- Los labradores pueden obtener dos dólares por bushel de patatas el primero de julio, y después el precio cae en dos centavos por bushel por día. El primero de julio un labrador tien 80 busheles de patatas en el campo y estima que la producción esta creciendo a un ritmo de un bushel por día. ¿Cuando debería recoger el labrador las patatas para maximizar los ingresos?
Ingreso = 80*2 dólares el primeo de julio X = días transcurridos
Precio = P = 2 – 0.02 X producción = Q = 80 +X
Ingreso total = IT = ( 2 – 0.02 X ) ( 80 +X )
I T = 160 + 2X – 1.6 X – 0.02 X2 = 160 –+0.4 X – 0.02 X2
Para encontrar el maximo ingreso debemos derivar el ingreso total.
 =
= 
→ 0.4 = 0.04 X → X = 10
Deberán de pasar 10 días desde el primero de julio para que alcance los máximos beneficios es decir deberá recoger las patatas el 11 de julio.
Para comprobar que son los máximos beneficios hallamos la segunda derivada que debe ser negativa.
- Una firma de plásticos ha recibido un pedido del departamento de recreo de la ciudad para fabricar 8000 tablas de polietileno para su programa de natación de verano. La firma posee diez máquinas, cada una de las cuales puede producir 30tablas por hora. El coste de puesta a punto de las maquinas para producir las tablas es de 20dolares por maquina. Una vez puestas a punto las maquinas, la operación es totalmente automática y puede ser supervisada por un supervisor de producción que gana 4.80 dólares por hora
a) ¿Cuantas maquinas deberían usarse para minimizar el coste de producción?
b) ¿Cuanto ganara el supervisor durante la marcha las maquinarias si se usa el numero optimo de maquinas?
c) ¿Cuanto costara poner a punto el número óptimo de maquinarias?
Solución
Total de tablas a fabricar = 8000
Total de maquinas = 10
Producción de cada maquina por hora = 30
Costo de puesta a punto = 20 * maquina
Costo del supervisor = 4.8 * hora
Numero de horas = X numero de maquinas = Y
30 * Y * X = 8000 → y = 
CT = 20 Y + 4.8 X
CT = 20 * + 4.8 X
+ 4.8 X
Para obtener el mínimo costo derivamos el costo total e igualamos a cero.
16000= 14.4 X2 → X = 33.3
Reemplazando X = 33.3 en Y , se obtiene Y = 8
Entonces se concluye que
a) se deberían usar 8 maquinas para poder minimizar el coste
b) lo que ganara el supervisor es 4.8 por hora esto es 4.8 * 33.3 , lo cual da como resultado 160 dólares.
c) El coste de poner a punto las maquinas es de 20dolares por maquina, esto es 20 * 8 , lo que resulta 160 dólares por todas las maquinas
- Una taberna local espera gastar 800 botellas de bourbon este año. El bourbon cuesta 4 dólares por botella, los gastos del pedido son de 10 dólares por cargamento y el costo de almacenaje del bourbon es de 40 centavos por botella cada año. El bourbon se consume a un ritmo constante a lo largo del año y cada cargamento llega justo cuando el cargamento anterior ha sido gastado.
a) ¿Cuántas botellas debe pedir el tabernero en cada cargamento para minimizar el coste?
b) ¿Con que frecuencia debe pedir el bourbon?
c) ¿Cómo cambian las respuestas a las partes a) y b) si el coste del bourbon aumenta a 4,30 por botella?
Costo = costo por + gastos del + costo de
Total botella pedido almacenaje
X = numero de botellas por pedido
Numero de pedidos = 
Promedio de almacenaje =  costo de almacenaje =
costo de almacenaje = 
CT = 4 ( 800 ) +  +
+
 → X2 =
→ X2 =  → X = 200
→ X = 200
Respuestas:
a) como x era el número de botellas por pedido, entonces concluimos que debe de pedir 200 botellas para obtener el mínimo costo.
b) Se sabe que el numero de pedidos viene dado por  , entonces reemplazamos. Y tenemos que el numero de pedidos debe ser 4
, entonces reemplazamos. Y tenemos que el numero de pedidos debe ser 4
c) Simplemente no varían, ya que al momento de derivar el aumento del precio no afecta a ninguna variable.
- Un camión esta alquilado para transportar mercancías desde una fabrica a un almacén. El salario del conductor ha sido fijado por horas y es así inversamente proporcional a la velocidad a la que conduce el camión.
La cantidad de gasolina gastada es directamente proporcional a la velocidad a la que conduce el camión, y el precio de la gasolina permanece constante durante el viaje. Demostrar que el coste total es menor a la velocidad para la cual el salario del conductor es igual al coste de la gasolina usada.
Sea P: precio de la gasolina (cste) X: nº de horas conducidas
G: nº de galones consumidos
Salario del conductor por horas: S = k1
V
Cantidad d gasolina gastada: G = k2 * v
Coste total = salario + gasolina
C = X * S + P * G → C = X *  + P * k2 * v
+ P * k2 * v
Se pide demostrar: X *  = P * k2 * v
= P * k2 * v
 = 0
= 0
 =
= 
→  =
=  que es lo que se quería demostrar
que es lo que se quería demostrar
 > 0 → mínimo costo
> 0 → mínimo costo
- Un fabricante de bicicletas compra 6000 llantas al año a un distribuidor y esta tratando de decidir la frecuencia de sus pedidos. Los gastos de pedido son de 20 dólares por cargamento, el coste de almacenaje es de 96 centavos por llanta y por año y cada llanta cuesta 25 centavos. Suponga que las llantas se usan a un ritmo constante a lo largo del año y que cada cargamento llega justo cuando el cargamento precedente ha sido terminado. ¿Cuantas llantas debería pedir cada vez el fabricante para minimizar el coste?
Coste = Coste de + coste de + coste de las
total Almacenaje pedidos llantas
X = nº de llantas por cargamento
C( X ) = coste total
Coste de = X ( coste de almacenar una llanta un año )
Almacenaje 2
Coste de = X ( 0.96 ) = 0.48 X
Almacenaje 2
Coste total = coste del pedido * número de
del pedido por cargamento cargamentos
Coste del pedido = 
Coste de = numero total * coste por
las llantas de pedidos llanta
Coste de = 6000 ( 0.25 ) = 1500
las llantas
C ( X ) = 
 → 0.48 =
→ 0.48 = 
X = 500
Para minimizar el coste, el fabricante debe pedir las llantas en lotes de 500
- Un almacén vende monopatines al precio de US$40 por unidad. A este precio las personas han comprado 50 monopatines al mes. El propietario del almacén desea aumentar el precio y estima que por cada incremento de US$1 en el precio se venderán 3 monopatines menos cada mes. Si cada monopatín tiene un costo de US$25 para el almacén, ¿a qué precio debería vender los monopatines para maximizar las utilidades?
SOLUCION
Se pide maximizar las utilidades, por lo que diseñaremos la ecuación que define las utilidades. Utilidad es igual a ingresos menos costos.
Cantidad de venta mensual = 50 - 3(x - 40)
Ingresos = x [ 50 - 3 (x-40)]
Costos = 25 [50 - 3 (x-40)]
Utilidad = (x-25) [50-3(x-40)= U = -3x2 + 245x + 450 y su derivavada es:
U` = -6x+245 = 0, de donde al despejar x, se tiene x= 245/6 = x= $41.00 que debe ser el precio de venta de los monopatines.
- Una librería puede obtener del editor determinado libro a un costo de US$3 por unidad. La librería ofrece el libro a un precio de US$15 por ejemplar y, a este precio, ha vendido 200 ejemplares por mes. La librería planea bajar el precio para estimular las ventas y calcula que por cada reducción de UN $1 en el precio se venderán 20 libros más cada mes. ¿A qué precio debería la librería vender el libro para generar la máxima utilidad posible?
SOLUCIÓN
Se pide maximizar las utilidades.
Cifras ofrecidas por el libro: Costo $3; Precio de Venta $x; utilidad = x-3
UITLIDAD TOTAL = [UTILIDAD POR LIBRO] * [CANTIDAD DE LIBROS VENDIDOS].
U = [200+20(15-x)][x-3] = (200+300-20x)(x-3) = U = 20 (-x2 +28x-75), que define la función de la utilidad y cuya derivada es:
U´ = 20 (-2x+28) = 0, de donde x = (28/2) = x = $14.00
- Un almacén de estampas de béisbol puede obtener las del novato Mel Schlabotnik un costo de $5.00 cada una. El almacén ofrece las estampas a $10.00 cada una y, a este precio, ha vendido 50 por mes. El almacén planea bajar el precio para estimular las ventas y estima que por cada 50 centavos de reducción en el precio se venderán 5 estampas más cada mes. ¿A qué precio debería vender el almacén para maximizar la utilidad total mensual?
SOLUCIÓN
Se pide maximizar las utilidades. Para el almacén se tiene un costo unitario de $5, un Precio de Venta actual de $10 y un precio de venta desconocido x. Decir 5 estampas por 50 centavos es lo mismo que 10 estampas por $1.00 de manera que:
La cantidad total de ventas es: 50 + 10 (10-x)
La Utilidad U = (x-5) [50 + 10 (10-x)] = (x-5) (50 + 100 - 10 x] = -10x² +200x-750.
Al derivarla se obtiene U´ = -20x + 200 = 0, de donde se despeja
x = 200/20 = x= $10.00
- Un cultivador de fritas cítricas de Florida estima que si plantan 60 naranjos la producción media por árbol será 400 naranjas, la cual disminuirá en 4 naranjas por árbol si se planta un árbol adicional en la misma área. ¿Cuántos árboles debería plantar el cultivador para maximizar la producción total?.
SOLUCION
Lo que se pide es maximizar la Producción, por lo que hallaremos la ecuación que describe la producción P.
Los árboles en total son 60 más los que se añadan, es decir, = 60 + x.
Cada árbol produce 400 menos 4 por árbol añadido, es decir, = 400 - 4x
La producción total P = [PRODUCCION POR ARBOL]*[TOTAL DE ARBOLES]= P = (400-4X) * ( 60 + X ) = -4X2 + 160x +2400, que al derivar para maximizar, da:
P'= -8x + 160 = 0; de donde al despejar x, se tiene x = 160/8 = 20 árboles encima de 60, de manera que el total es 60+20 = 80 árboles se deben plantar.
Cada árbol dará 400 - 4x, o sea 400 - (4)(20) = 320 naranjas con lo que se tendrán un máximo de (80 árboles) por (320 naranjas), 25600 naranjas como producción máxima.
- Una empresa de plásticos ha recibido un pedido del departamento de recreación de la ciudad para fabricar 8,000 tablas de plástico para su programa veraniego de natación. La empresa posee 10 máquinas, cada una de las cuales puede producir 30 tablas por hora. El costo de puesta en marcha de las máquinas para producir las tablas es US$20 por máquina. Una vez puestas en marcha las máquinas, la operación es totalmente automatizada y puede ser vigilada por un solo supervisor de producción que gana US$4.80 por hora. ¿Cuántas máquinas deberían emplearse para minimizar el costo de producción?
SOLUCIÓN
El costo de la puesta en marcha es 20x. El costo de operación es 1280/x.
Horas = 8,000 tablas / 30 tablas por hora = 266.66 horas que a $4.80 dan $1,280.00
CT = 20x + 1280/x y su derivada es CT' = 20 - (1280/x²) = 0
1280/x² = 20
x²=128/2
x = sqr(64) = 8 máquinas
a) ¿Cuánto ganará el supervisor durante la jornada de producción si se utiliza el número óptimo de máquinas?
Si x= 8, Costo óptimo = 1280/x = $160.00
b) ¿Cuánto costará poner en marcha el número óptimo de máquinas?
20x = 20(8) = $160.00
- Suponga que la demanda q y el precio p de cierto articulo están relacionadas por la ecuación: q = 300 – p2 ( para
 )
)
a) Determine donde la demanda es elástica, inelástica y de elasticidad unitaria con respecto del precio.
b) Utilice los resultados del literal a) para describir el comportamiento del ingreso total como una función del precio.
c) Halle la función del ingreso en forma explicita y emplee la primera derivada para determinar sus intervalos de crecimiento y decrecimiento y el precio al cual se maximiza el ingreso.
Solución
a)La elasticidad de la demanda es
La demanda es de elasticidad unitaria cuando  , es decir, cuando
, es decir, cuando
Del cual solo p = 10 esta en el intervalo pertinente  , si
, si
 ,
,
Y por consiguiente la demanda es inelástica
Si 
Y por consiguiente la demanda es elástica.
b) el ingreso total es la función creciente de p cuando la demanda es inelástica, es decir esta en el intervalo  y una fracción decreciente de p cuando la demanda es elástica, esto es este es el intervalo
y una fracción decreciente de p cuando la demanda es elástica, esto es este es el intervalo  . Al precio de p = 10 de elasticidad unitaria, la función del ingreso tiene un máximo relativo.
. Al precio de p = 10 de elasticidad unitaria, la función del ingreso tiene un máximo relativo.
|
Curva de ingreso
R(p)
R(p) = p ( 300 – p2)
10  p p
|
C) la función de ingreso es r = p q
· R(p) = p ( 300 – p2) = 300p – p3
Su derivada es
R´(p) = 300 – 3p2 = 3 ( 10- p ) ( 10 + p )
Que es cero cuando p =  10, del cual solo p = 10 esta en el intervalo pertinente
10, del cual solo p = 10 esta en el intervalo pertinente  .
.
En el intervalo  , R´( p) es positiva y por lo tanto R(p) es creciente.
, R´( p) es positiva y por lo tanto R(p) es creciente.
En el intervalo  , R´( p) es negativa y por lo tanto R ( p ) es decreciente. En el valor critico p=10 , R(p) deja de ser creciente y comienza a ser decreciente y por consiguiente tiene un máximo realtivo.
, R´( p) es negativa y por lo tanto R ( p ) es decreciente. En el valor critico p=10 , R(p) deja de ser creciente y comienza a ser decreciente y por consiguiente tiene un máximo realtivo.
Curva de demanda
 q q
300
Q = 300 – p2
10  p p
|
INTEGRALES
- Una inversión producirá 2400 dólares al año a perpetuidad, si el dinero se dispensa continuamente a lo largo del año y el tipo de interés anual predominante permanece fijo al 12 por 100 compuestos continuamente. ¿Cuál es el valor actual de la inversión?
Valor actual de la inversión= 2400 
V.A =  =
= 
V.A =  =
=
V.A = 0 +20000 = 20000
El valor actual de la inversión será de 20000 dólares con una tasa de interés de 12% .
- Use una integral definida para estimar el valor actual de una anualidad que paga 100 dólares por mes en los próximos 2 años. Si el tipo de interés que prevalece permanece fijo a un 8 por 100 anual compuesto continuamente.
Valor actual de la anualidad = 
- Un donante quiere hacer una donación a un colegio público de la cual puede retirar el colegio 7000 dólares al año a perpetuidad para soportar el funcionamiento de su centro de cálculo. Suponiendo que el tipo de interés anual predominante permanece fijo al 14 por 100compuesto continuamente. ¿Cuanto debería dar el donante al colegio? Esto es ¿Cuál es el valor actual de la donación?
- La cantidad demandada K (en unidades de centena) de las cámaras miniatura MIKADO cada semana se relaciona con el precio unitario y ( en dólares ) como Y = f ( x) = -0.2 x2 + 60, por otro lado la cantidad x ( en unidades de centena ) que el proveedor esta dispuesto a poner a la venta se relaciona con el unitario y en ( dólares ) de la forma Y = g ( x) = 0.1 x2 + x + 40. Si el precio de mercado se establece como el precio de equilibrio, determine el excedente de los consumidores y de los productores.
Sea f ( x) = -0.2 x2 + 60 la demanda del mercado
y g ( x) = 0.1 x2 + x + 40 la oferta de mercado
en equilibrio se cumple que f ( x) = g ( x)
→ -0.2 x2 + 60 = 0.1 x2 + x + 40
0.3 x2 + x – 40 = 0 → 3 x2 + 10 x – 400 = 0
x1 = 10 y x 2 = - 13.33
→ en equilibrio x = 10 y P= 60
 Excedentes del consumidor y el productor Excedentes del consumidor y el productor
oferta
E
60
demanda
10 Q
|
Excedente del consumidor = 
E.C = 
EC = 
EC = ( -66.6 + 800 ) – 600
EC = 733.3 - 600 = 133.3 excedente del consumidor
Excedente del productor = 
EP = 
EP = 
EP = 
EP = 600 - 483.3 = 116.6 excedente del productor
- Se estima que dentro de t años una cierta inversión que generara ingresos a un ritmo de f( t ) = 8000 + 400 t dólares por año. Si los ingresos se generan a perpetuidad y el anual de intereses predominante permanece fijo a un 10 por 100 compuestos continuamente. Halle el valor actual de la inversión.
Solución:
Si los ingresos son: f( t ) = 8000 + 400 t
Valor actual: ( 8000 + 400 t ) e-0.1 t
V.A = 
V.A = 
V.A =  por partes
por partes
V.A = 
V.A = 
V.A = 
V.A = -80000( 0 – 1 ) + 400 ( 0 – (-100))
V.A = 80000 + 40000 = 120000
- Un fabricante de bicicletas espera que dentro de x meses los consumidores estaran comprando 3000 bicicletas por mes a un precio de P ( x) =
 dólares por bicicleta ¿ cual es el ingreso que el fabricante puede esperar de la venta de bicicletas en los próximos 24 meses?
dólares por bicicleta ¿ cual es el ingreso que el fabricante puede esperar de la venta de bicicletas en los próximos 24 meses?
Qconsumidores = 3000 precio : P ( x) = 
Ingreso total = I T = Qc* P(x)
I T = 3000* 
IT = 
I T = 
I T = 
I T = 3000 ( 1920 + 235.15)
I T = 6 465 453.046
Cuando una empresa genera un flujo de ingresos durante cierto periodo (por ejemplo; un plazo de 5 años) al obtener los ingresos estos se vuelven a invertir y ganan intereses con una tasa fija. El flujo de ingresos acumulados futuros durante periodo de cinco años es la cantidad de dinero que obtiene la empresa al fin de ese periodo. La integral de finida se utiliza para calcular el flujo de ingresos futuros totales o acumulados durante cierto tiempo.
Si: R (t) = Tasa de generación de ingresos en cualquier momento t.
r = Tasa de Interés compuestas en forma Continua
0 t1 t2 t3 ..... tn-1 tn = T
Figura 1.1
El intervalo de tiempo [o,t] se divide en n intervalos con la misma longitud Dt = t/n además tn = t como se muestra en la figura 1.1
Si R es la función continua en el intervalo [o,t] entonces R(t) no será muy distinta de R (t1) en el intervalo [o,t1] siempre que éste sea pequeño. Debido a esto el ingreso generado durante el intervalo [o,t1] es aproximadamente:
A1 = R (t1) Dt dólares
El valor futuro de esta cantidad, dentro de T años, calculando como si se ganase en el instante T1 es:
A1=[R(t1)Dt]e=r(T-t1).
Los mismos ocurre con los ingresos durante el intervalo [t1,t2] que obtiene una valor futuro dentro de T años, de [R(t2)Dt]er(T-T2) dólares
Es por ello que la suma de todos los valores futuros generados durante el periodo [O,T] es:
A = R(t1)er(T-T1)Dt+R (t2)er(t-t2) DT T…T R(Tn)er(T-Tn) Dt
A = er(T) [R(t1)e-rt1 Dt1+R(t2)e-rt2 Dt+ ... t R(tn)e-rtn Dt]
La suma anterior es la suma Rieman de la función ert R(t)e-n en el intervalo [o,t] que esta dividido en T1, T2...Tn.
Cuando n tiene al infinito se obtiene el valor futuro total después de un periodo de T años, de un ingreso R (t) dólares por años que gana intereses a razón de r por año:
A = 

34. Recientemente Texano compró una máquina automática para el lavado de autos que se espera que genere $80,000 de ingreso por año durante los próximos años. Si los ingresos se reinvierten y texano genera intereses a razón de 10% por año compuestos en forma continua, determinar el valor total acumulado de este flujo de ingresos al cabo de cinco años.
SOLUCIÓN:
R(t) = 80,000
R = 0.10
T = 5
A = e0.10(T)
A= eo.T.80,000
El valor futuro de la inversión en cinco años será 518 977
35. El dinero se transfiere continuamente a una cuenta a razón constante de US$ 1,200 por año. La cuenta gana intereses a razón anual de 8% capitalizado continuamente ¿Cuánto habrá en la cuenta al cabo de 2 años?
Para aproximar el valor futuro del flujo de ingresos, es necesario dividir el intervalo de tiempo de 2 años 0 £ t £ en n subintervalor iguales de longitud Dnt años
SOLUCIÓN 2-tj años
 1,200Dnt 1200e0.08(2-tj)
1,200Dnt 1200e0.08(2-tj)
t1 tj tj+1
Dinero depositado = (dólares al año) (numero de años) = 1200 An
*** se depositará todo el dinero al comienzo del intervalo en el tiempo tj, permanecería en la cuenta por 2-tj años y todo crecería a (1200 Dnt) e0.08(2-tj) dólares
Valor Futuro del =
flujo de ingresos
Al cabo de 2 años habrá en la cuenta 2602.66 dólares
Es otra forma de calcular el valor de un flujo de ingresos es considerar su valor presente.
El valor actual de un flujo de ingresos generado continuamente a cierta tasa durante un periodo específico es la cantidad de dinero que debe depositarse hoy en día a la tasa de interés predominante para generar el mismo flujo de ingresos durante el mismo periodo.
36. Un exitoso empresario textil esta considerando dos planes alternativos para mejorar su producto. El plan A requiere de un desembolso inmediato de $ 350,000, mientras que el plan B necesitará un desembolso inmediato de $280,000. se ha estimado que la adopción del plan A significaría un flujo neto de ingresos generados a razón de:
Y para el plan B representaría un flujo neto de ingresos a razón de:
g(t)=680,000 dólares
Durante los próximos tres años. Si la tasa de interés durante los próximos 5 años fuese de 10% por año ¿Cual plan que más le más le conviene al empresario?
I) Plan A requiere 350,000 dólares
R (t) = 730,000
r = 0.1
t = 3 años
Plan B: requiere 280,000 dólares
R(t)=680,000
r = 0.1 
t = 3 años
Pv = 
Respuesta: El Plan A es el plan que más le resulta al empresario
37. Suponga que se espera que una inversión genere ingresos a razón de:
R (t) = 200,000 por año
Durante los próximos cinco años. Encuentra el valor presente de una inversión si la tasa interés predeciente es de 8% por año compuesta en forma continua.
SOLUCIÓN:
r = 0.08
t = 5 años
El valor presente de la inversión será 824 200
38. La gerencia de una cadena nacional de heladerías esta vendiendo una franquicia de 5 años para operar un nuevo punto de venta en Sullana – Piura. La experiencia anterior en sitios semejantes indica que dentro de y años la franquicia generará una utilidad a razón de f(t)= 14,000 + 490t dólares al año. Si la tasa de interés anual predominante permanece fija durante los próximos 5 años, 7% capitalizado continuamente, ¿Cuál es el valor presente de la franquicia?
Para aproximar el valor presente de la franquicia es necesario dividir el intervalo de 5 años o £ t £ 5 en n subintervalos iguales de longitud Dnt años.
SOLUCIÓN:
 Tj años
Tj años 
t1 tj tj+1
El valor actual de la franquicia es 63,929.41
- La cantidad demandada K ( en unidades de centena ) de las cámaras miniatura MIKADO cada semana se relaciona con el precio unitario y ( en dólares ) como Y = f ( x) = -0.2 x2 + 60, por otro lado la cantidad x ( en unidades de centena ) que el proveedor esta dispuesto a poner a la venta se relaciona con el unitario y en ( dólares ) de la forma Y = g ( x) = 0.1 x2 + x + 40. Si el precio de mercado se establece como el precio de equilibrio, determine el excedente de los consumidores y de los productores.
Sea f ( x) = -0.2 x2 + 60 la demanda del mercado
y g ( x) = 0.1 x2 + x + 40 la oferta de mercado
en equilibrio se cumple que f ( x) = g ( x)
→ -0.2 x2 + 60 = 0.1 x2 + x + 40
0.3 x2 + x – 40 = 0 → 3 x2 + 10 x – 400 = 0
x1 = 10 y x 2 = - 13.33
→ en equilibrio x = 10 y P= 60
 Excedentes del consumidor y el productor Excedentes del consumidor y el productor
oferta
E
60
demanda
10 Q
|
Excedente del consumidor = 
E.C = 
EC = 
EC = ( -66.6 + 800 ) – 600
EC = 733.3 - 600 = 133.3 excedente del consumidor
Excedente del productor = 
EP = 
EP = 
EP = 
EP = 600 - 483.3 = 116.6 excedente del productor
- Se estima que dentro de t años una cierta inversión que generara ingresos a un ritmo de f( t ) = 8000 + 400 t dólares por año. Si los ingresos se generan a perpetuidad y el anual de intereses predominante permanece fijo a un 10 por 100 compuestos continuamente. Halle el valor actual de la inversión.
Solución:
Si los ingresos son: f( t ) = 8000 + 400 t
Valor actual: ( 8000 + 400 t ) e-0.1 t
V.A = 
V.A = 
V.A =  por partes
por partes
V.A = 
V.A = 
V.A = 
V.A = -80000( 0 – 1 ) + 400 ( 0 – (-100))
V.A = 80000 + 40000 = 120000
- Un fabricante de bicicletas espera que dentro de x meses los consumidores estaran comprando 3000 bicicletas por mes a un precio de P ( x) =
 dólares por bicicleta ¿ cual es el ingreso que el fabricante puede esperar de la venta de bicicletas en los próximos 24 meses?
dólares por bicicleta ¿ cual es el ingreso que el fabricante puede esperar de la venta de bicicletas en los próximos 24 meses?
Qconsumidores = 3000 precio : P ( x) = 
Ingreso total = I T = Qc* P(x)
I T = 3000* 
IT = 
I T = 
I T = 
I T = 3000 ( 1920 + 235.15)
I T = 6 465 453.046
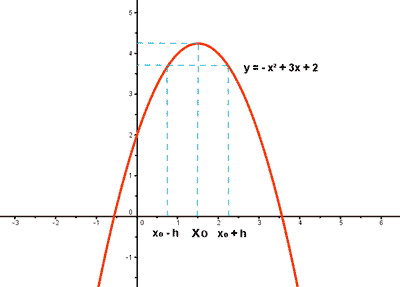
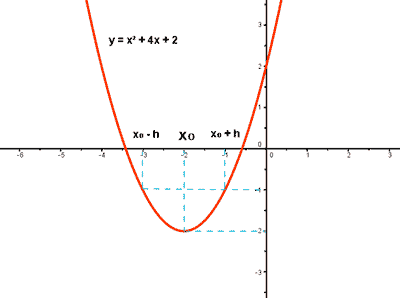
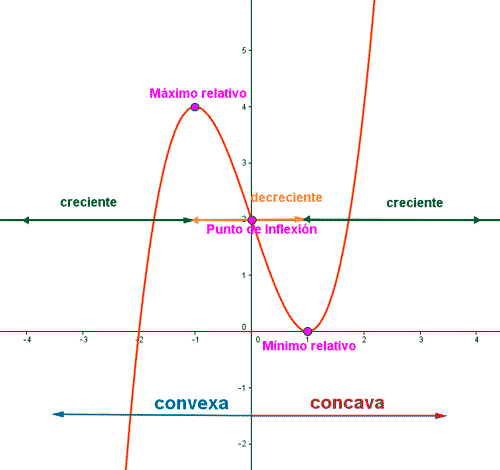
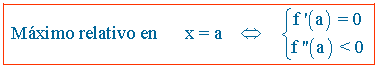
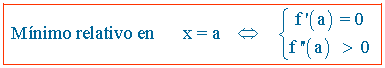

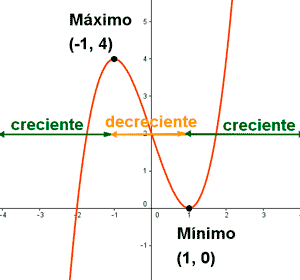
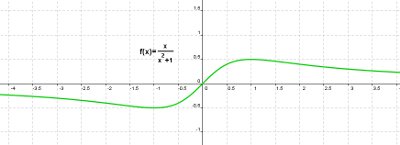 El segundo paso, fue repasar las que llamábamos funciones elementales, y recordar cómo se representaban pues a partir de la gráfica lo sabíamos todo, pero claro, hay muchas más funciones, y sería interesante saber también cómo es la forma de todas ellas. La expresión algebraica o analítica nos da la exactitud, pero la expresión gráfica es la que nos aporta visualmente gran información. Por ejemplo, si tenemos la función
El segundo paso, fue repasar las que llamábamos funciones elementales, y recordar cómo se representaban pues a partir de la gráfica lo sabíamos todo, pero claro, hay muchas más funciones, y sería interesante saber también cómo es la forma de todas ellas. La expresión algebraica o analítica nos da la exactitud, pero la expresión gráfica es la que nos aporta visualmente gran información. Por ejemplo, si tenemos la función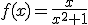
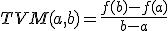
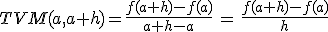
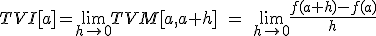
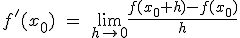
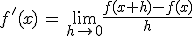








 y como
y como 














 = 0
= 0 > 0 → mínimo costo
> 0 → mínimo costo

 → 0.48 =
→ 0.48 = 





 =
=












 por partes
por partes














