LOS SISTEMAS DE
NUMERACIÓN
Para representar un número
necesitamos un sistema, que, mediante ciertas reglas y principios, permitan
hacerlo adecuadamente. Es por eso que ahora aprenderemos como a partir de la
idea Inicial, lograremos simbolizarlo.
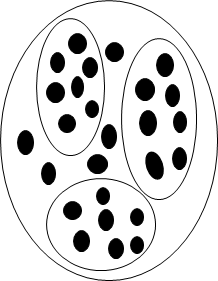
Tenemos el siguiente gráfico:
Si nos preguntan
cuántos elementos tiene, lo prmero que hacemos es contar y de ese conteo obtenemos 26 que es la
representación simbólica del total de
elementos.
La pregunta es
¿porqué 26? es decir, ¿porqué 2 y 6 juntos?
La respuesta es
que se está usando el sistema decimal de base 10 para representar esta
cantidad, mejor dicho, se agrupan los elementos de 10 en 10 (valor de la base)
y vamos a obtener 2 grupos completos
de 10
y 6 elementos sobrantes.
Considerando este razonamiento si los mismos elementos lo representásemos en el sistema de base 7 en tonces la agrupación quedaría así: 3 grupos completos de 7 elementos y 5 elementos sueltos y su representación sería 35 en el sistema de base 7 o abreviado: 357
Esto nos lleva a deducir el método para poder representar un número en cualquier sistema de numeración, ya que si hablamos de “agrupar” entonces es fácil saber que, la operación correspondiente es la DIVISIÓN entonces nos falta
saber que hacemos si la cantidad de “grupos” es mayor que el valor de la
base del sistema de numeración, veamos el mismo ejemplo pero usando el sistema
de base 3 , se tendría 8 grupos y 2 elementos sueltos,entonces se agruparía
así:
Entonces se escribiría así:
2 “grupos grandes”
2 “grupos medianos”
2 “elementos sueltos”
El numeral sería:
222(3)
El agrupar nos lleva a la
Operación de DIVISIÓN
Tomamos el último cociente y todos
los residuos anteriores entonces: 222(3)
En conclusión:
26 del sistema de base 10 se puede
representar como: 35(7) y 222(3)
26 =35(7) = 222(3)
Ahora como comprobamos que: 35(7) y 222(3)
son iguales a 26, la lógica nos dice que para llegar a la representación
en base 7 y base 3 hemos dividido y en ese proceso de la división también se ha
restado, lo único que debemos hacer es usar las operaciones contrarias, es
decir,multiplicación y adición y lo haremos de la siguiente manera:
- Colocamos las cifras del número separadas y la base en la parte inferior izquierda en esta disposición:
- Luego bajamos la primera cifra de la izquierda para empezar con las operaciones antes mencionadas (Multiplicación y adición):
El número obtenido es 26, con el cual hemos realizado los ejercicios
anteriores.
Así es el método de Ruffini, que lo
hemos deducido desde la noción inicial, pero no es el único también podemos
utilizar la descomposición polinómica que es una forma abreviada del método
de Ruffini:
Se multiplica cada cifra por el valor de la base y cada base tendrá un
exponente, empezando con cero para la base que multiplica a la última cifra y
sucesivamente colocamos: 1;2;3;…..como exponente para cada base que multiplica a las cifras
que se encuentran a la izquierda de la última:
222(3) = 2x32+2x31+2x30
Entonces:
- Para convertir un número del sistema de base 10 a otro sistema dividimos en forma sucesiva
- Para convertir un número de un sistema de base cualquiera a base 10 lo que podemos aplicar es el Método de Ruffini o la descomposición Polinómica
Ahora la última pregunta: ¿Y si queremos convertir un número de un
sistema diferente de base 10 (o sistema decimal) a otro también diferente de
base 10?
La pregunta es sencilla de responder si analizamos los casos anteriores:
- Tenemos el número escrito en una base” m” (diferente de 10) y queremos pasarlo a base “n” (también diferente de 10)
- Primero, el número de base “m” lo pasamos a base 10 por Ruffini o descomposición polinómica.
- Segundo, el resultado obtenido en base 10 lo convertimos a base “n” por divisiones sucesivas.
Ejemplo:
Convertir: 164(7) al sistema de base 4
Primero: 164(7) a base 10
164(7) = 1x72+6x71+4x70=
49+42+4= 95
Segundo: 95 a base 4