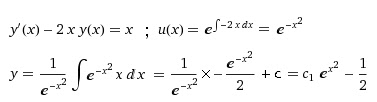Ecuaciones Diferenciales
Esta materia es una de las más odiadas en muchas carreras. Ya que a mi me tocaron maestros de mierd* que no sabían nada y no se les entendía ni madres, tuve que investigar mucho para para aprender esto y poder pasar la materia. El objetivo de este post es explicar los principales métodos para resolver Ecuaciones Diferenciales Ordinarias de forma fácil y entendible. Con sólo anotar algunas fórmulas, formas y conceptos, las ecuaciones se volverán más claras y su respuesta será más accesible. Empecemos.
Una ecuación diferencial es aquella ecuación que contiene derivadas, punto. Las ecuaciones diferenciales ordinarias contienen derivadas de funciones que dependen de una sola variable independiente. Una ecuación diferencial se considera resuelta cuando se ha reducido a una expresión en términos de integrales, puedan o no resolverse las mismas.
Clasificación
Las Ecuaciones Diferenciales Ordinarias se dividen en lineales y no-lineales. Son lineales si todos sus términos son lineales respecto a la variable dependiente y sus derivadas. De lo contrario, no es lineal. Recordemos que para que un término sea lineal, debe estar expresado de forma que al graficarlo nos quede una línea recta. Osea que y², y³, e^y, log(y) NO son lineales. Así mismo, las EDO se dividen en homogénea y no homogénea. Es homogénea si no contiene términos que dependen únicamente de su variable independiente. Ejemplos.
Ecuaciones Diferenciales de 1er orden
Una ecuación diferencial ordinaria de primer orden es una ecuación diferencial ordinaria donde intervienen derivadas de primer orden respecto a una variable independiente. Osea que, en geometría analítica, tendrían la forma de las ecuaciones de primer grado. Éstas son las ecuaciones diferenciales más sencillas y no se necesitan muchos cálculos. Existen básicamente 7 formas en que se presentan estas ecuaciones de primer orden, en las cuales no se hace más que aplicar álgebra y cálculo elemental.
1.
ECUACIÓN DIFERENCIAL SEPARABLE y' = F(x, y). General
Esta forma es la más fácil de las Ecuaciones Diferenciales. Lo único que tenemos que hacer es acomodarla de tal forma que en un lado de la igualdad nos quede dx y del otro dy con sus respectivas variables. Es separable si el segundo miembro de la diferencial la podemos expresar como el producto de 2 funciones. Una que dependa solo de la variable dependiente y otra que contenga sólo la variable independiente. O sea: y'= f(x)*g(x)
Ejemplo.
Ya que en este caso nos quedó la variable dependiente despejada, le llamamos a esta solución explícita. La solución debe quedar en lo posible de esta forma, aunque se dan casos donde la variable dependiente no puede quedar despejada; a dicha solución la llamaremos implícita. Algunos maestros tienen la puta costumbre de comprobar el resultado, derivando la solución y reemplazarla en la ecuación original para cerciorarnos de que se cumple. Aquí no pongo algún ejemplo porque es muy fácil, pero tengamos en cuenta que se llega a complicar en ecuaciones diferenciales de orden superior.
2. ECUACIÓN DIFERENCIAL LINEAL y' + P(x)y = g(x) -no es separable
a) Método de factor integrante Entonces lo único que vas a hacer es utilizara esta formulita:

Ejemplo:
b) Método de variación de parámetros Cuando encontremos una ecuación que tenga la forma
y' + p(x)y = g(x); g(x) = 0 aplicamos esta otra fórmula:

Ejemplo:
Nótese que esta ecuación se pudo resolver también por el método de factor integrante, obteniendo el mismo resultado.
3. ECUACIÓN EXÁCTA M(x,y)+N(x,y)y' = 0 Es exácta cuando My = Nx. La solución de esta ecuación tiene la forma Φ(x,y)=c, tal que Φx=M y Φy=N. Esta es la definición clásica para resolver este tipo de ecuación, pero como no se le entiende un carajo veamos un ejemplo.
 -Ecuación exácta con factor integrante
-Ecuación exácta con factor integrante Si M(x,y)+N(x,y)y' = 0 no es exácta, puede que
u*[M(x,y)+N(x,y)y'] = u*0 sea exácta. Para esto se debe cumplir que (uM)y=(uM)x
Lo que haremos será utilizar una de las siguientes 2 fórmulas de factor integrante, dependiendo de la variable que queramos utilizar.

Ejemplo:
4. ECUACIÓN DE BERNOULLI y'+p(x)y = q(x)y^n. En esta ecuación lo que haremos será sustituir
v=y^1-n, y multiplicar la derivada de v a todos los términos de la ecuación original para que nos quede una ecuación lineal.
Ejemplo.
5. ECUACIÓN DIFERENCIAL HOMOGÉNEA y' = F(x,y) Si el segundo miembro de la ecuación se puede expresar como y/x, se realiza la sustitución
v= y/x → y =v x → dy/dx = v + x dv/dx, la cual transforma la ecuación homogénea en separable. Ejemplo.
6. ECUACIÓN DIFERENCIAL CON COEFICIENTES LINEALES. (a1x + b1y + c1)dx + (a2x + b2y + c2)dy = 0 Esta es una de las forma más perras de las Ecuaciones Diferenciales, ya que tienes que hacer muchas cosas para llegar a la mentada solución. Pero con repasar muy bien el procedimiento y asegurarte de no cagarla en los detalles, podrás resolver este tipo de ecuaciones diferenciales.
1) Primero te tienes que asegurar de 2 cosas: que a1, a2, b1. b2, c1. c2 pertenecen a los números reales y que se cumpla la siguiente desigualdad a1*b2 ≠ a2*b1
2) Acomodas la ecuación tal que te quede de forma homogénea.
3) Sustituyes
dy/dx = dv/du 4) Sustituyes
x = u+h; y = v+k; donde u,v son variables, h,k son constantes.
5) Formas un sistema de ecuaciones con h + k + constante del numerador y el denominador. Si los valores encontrados en h, k satisfacen la igualdad a 0, entonces hemos llegado a una ecuación homogénea.
Aquí lo vemos más claro. En realidad no es tan complicado:
7. ECUACIÓN DIFERENCIAL DE LA FORMA y' = G(ax+ by) (no recuerdo el nombre)
Si el segundo miembro de la ecuación y' = F(x, y) se puede expresar en función de ax + by, o sea y' = G(ax+ by), entonces se realiza la sustitución
z = ax + by, la cual convierte la Ecuación Diferencial en separable.
-Ecuaciones Diferenciales lineales en series de potencia Las Ecuaciones Diferenciales pueden ser resueltas mediante series de potencia. La solución debe estar alrededor de un punto ordinario y no singular, esto se verifica observando el coeficiente de la derivada de mayor orden. Supongamos que tenemos la siguiente Ecuación Diferencial:
P(x)y'' + Q(x)y' + R(x)y = 0 Entonces:
-xo es un punto ordinario ↔ P(xo) ≠ 0
-xo es un punto singular ↔ P(xo) = 0
Para resolver Ecuaciones Diferenciales en series de potencia, utilizamos la serie de Taylor:


Lo que haremos será lo siguiente:
- Con el punto ordinario que nos han dado, suponemos la solución en series de potencia.
- Derivamos la solución y la reemplazamos en la ecuación diferencial
- Hacemos los cálculos pertinentes para que la ecuación diferencial nos quede en términos de una sola sumatoria.
- Obtenemos la fórmula de recurrencia
- Evaluamos
n veces la fórmula para obtener los valores constantes.
- Expandimos la Ecuación Diferencial en series de potencia y la evaluamos "n" veces, sustituyendo los valores constantes.
- Y ya.
Ejemplo.
Cuando expresamos la Ecuación Diferencial en términos de series de potencia, se considera resuelta, pero como aquí coincide con el número e, lo ponemos pa' ahorrarnos espacio; aunque es importante aclarar que no todas estas soluciones en sumatorias convergen hacia una función en particular.
Así mismo, habrá situaciones donde la ecuación no se podrá expresar como una sumatoria, sino que tendremos que poner término a término en la ecuación. Esto no tiene especial importancia en las Ecuaciones Diferenciales lineales, pero se complica en las Ecuaciones Diferenciales de orden superior que veremos después.
TOMADO :
http://www.taringa.net/posts/ciencia-educacion/13410677/Ecuaciones-Diferenciales-para-principiantes.html