Permítanme que comience haciéndoles una pregunta: de los dos segmentos que aparecen en la figura de la derecha, ¿cuál es el más largo?
A primera vista parece que el segmento mayor es el B, pero si prestan atención y se fijan bien podrán comprobar como por muchas vueltas que le den el segmento B sigue pareciendo mayor que el A.
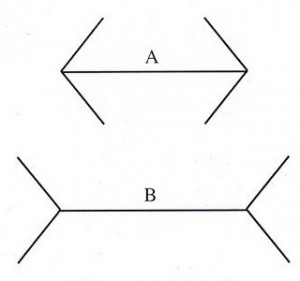
Sin embargo, por extraño que les parezca, lo que está llegando a sus ojos es una imagen en la que aparecen dos segmentos que tienen exactamente la misma longitud (compruébenlo aquí), aunque por culpa de las flechas dibujadas en los extremos lo que vemos es que el segmento de arriba es menor que el de abajo. Y lo más curioso es que seguiremos viéndolo así aunque sepamos que estamos equivocados.
Este conocido ejemplo de ilusión óptica viene como anillo al dedo para ilustrar un curioso problema que nuestro cerebro no es capaz de interpretar correctamente, por lo que podríamos decir que se trata de una especie de ilusión matemática.
Se trata de comparar el tamaño de dos conjuntos muy concretos, en el sentido de averiguar cuál de ellos tiene más elementos. El primer conjunto será N, el de los números naturales, que son aquellos con los que podemos contar cosas: 1, 2, 3, 4, … , que como supongo que sabrán tiene una cantidad infinita de elementos. El segundo conjunto es el formado por todas las parejas de números naturales que podamos hacer, es decir, el (1,1), el (1,2), o el (84,123312) por ejemplo, que obviamente también es un conjunto infinito y que llamaremos NxN. ¿Cuál de los dos conjuntos tiene más elementos?
Veamos que nos dice la intuición. Si llamamos ω al número de elementos del conjunto de los números naturales, como cada número natural aparece en NxN emparejado con todos los demás parece lógico pensar que este segundo conjunto tiene bastantes más elementos que el primero, tantos como resulte de multiplicar ωxω. Es decir, nuestro cerebro nos dice que NxN debe tener ω veces más elementos que N, y por tanto tiene que ser muchísimo mayor.
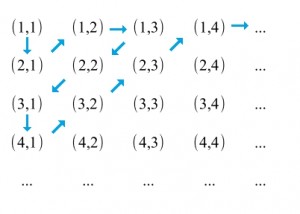
Sin embargo podemos demostrar fácilmente no sólo que esto no es cierto, sino que ademásambos conjuntos tienen exactamente el mismo número de elementos. Si ordenamos los elementos de NxN en una tabla donde en la primera fila aparezcan los elementos que empiezan con el 1, en la segunda los que lo hacen con el 2, etcétera; y disponemos las columnas de la misma manera, podemos escoger los elementos de NxN siguiendo el orden que indican las flechas:
Comprobamos entonces cómo los elementos de NxN pueden ordenarse de tal forma que (1,1) es el 1º, (2,1) es el 2º, (1,2) es el tercero, (1,3) el cuarto y así sucesivamente. Esto significa quepodemos contar todos elementos de NxN, y como contar es asignar números naturales, a cada elemento de NxN se le puede asignar otro de N. Por tanto, al contrario de lo que pensábamos, ambos conjuntos tienen el mismo número de elementos, o dicho de otro modo ωxω=ω.
Así, aunque nuestro cerebro nos dice que ambos conjuntos no son iguales, la lógica nos demuestra que lo son. Y por mucho que intenten convencerse de ello, no es posible hacerse una imagen en la cabeza de cómo pueden tener los mismos elementos dos conjuntos cuando uno de ellos se construye a partir de los ladrillos del otro, aunque sí se pueda comprender la lógica de la demostración.
En definitiva este problema nos muestra que el cerebro humano es imperfecto, hasta el punto de que nuestra imaginación sí tiene límites. Y si no se lo creen, fíjense en las películas que ha sacado Hollywood en los últimos diez años y después me cuentan.
Javier Oribe
TOMADO DE: http://www.hablandodeciencia.com/articulos/2011/10/07/una-ilusion-matematica/